时间序列分析 - 滑动窗口和 STL 分解
#data-science #时间序列分析 52

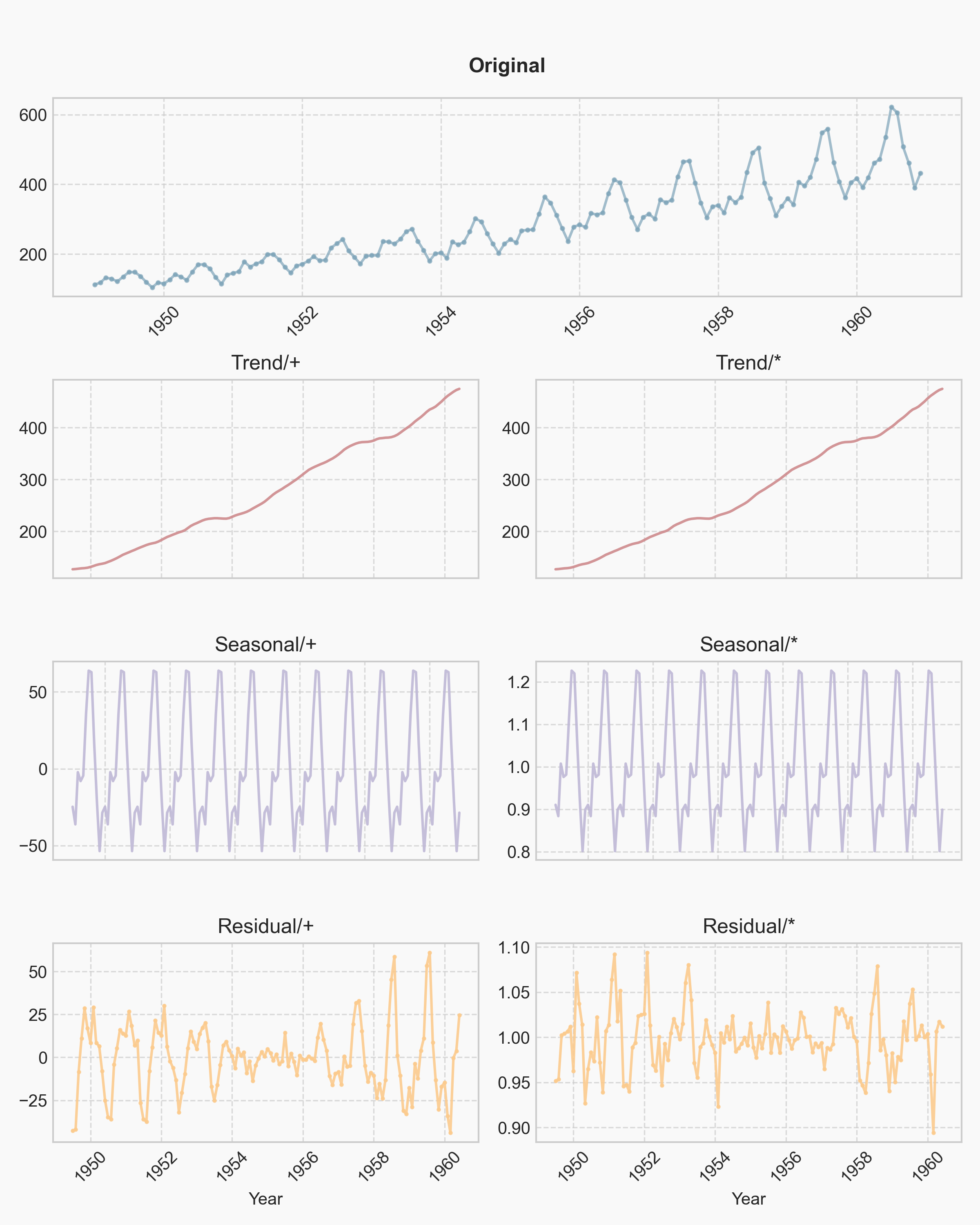
Fig.1 对 AirPassengers 数据进行 STL 分解的结果

前置

对于一组时间序列 Y_t，关注到序列的季节周期性，我们便认为它的基本成分包括：

  • 趋势 T_t (Trend)：序列总体而长期的变化特征；

  • 周期性 S_t (Seasonal)：随外部因素而周期性变化的特征，称之 Seasonal 是由于很多时候是季节造成这一周期性；

  • 随机扰动 R_t (Residual)：残差。

并随之存在两种分解方式：

  • 加法分解 Y_t = T_t+S_t+R_t，如果我们认为三个成分是相互独立互不影响的；

  • 乘法分解 Y_t=T_t * S_t * R_t，如果我们认为三个成分相关。

例子 A

构造一组 Y_t=10+X+10\sin{X}+\text{np.normal(0, 1)}，再对其进行乘法分解，得到结果：

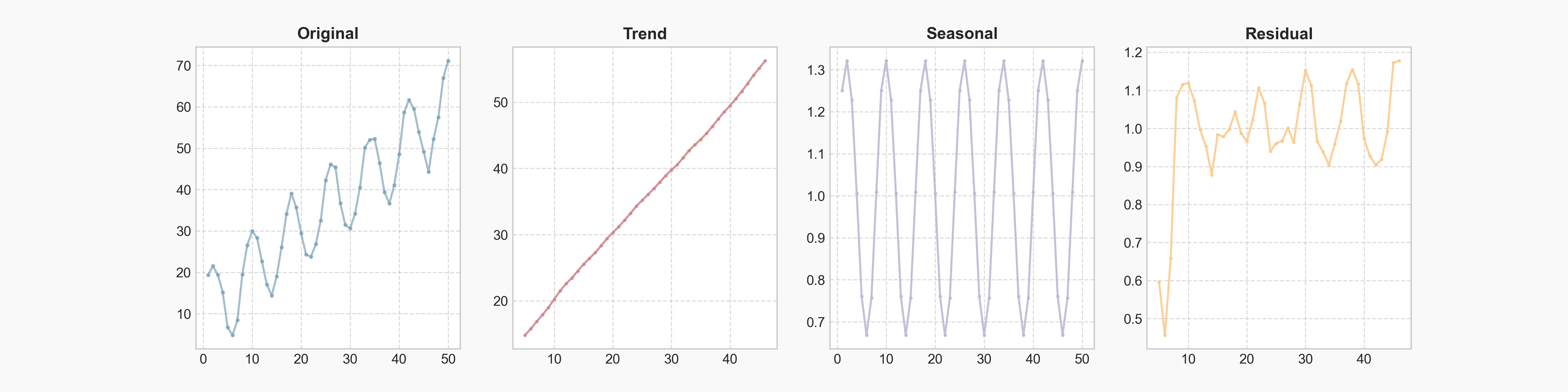
Fig.2

Residual 尺度大到和 Seasonal 相近了，看起来也与 Seasonal 颇相关，所以乘法分解应该不是太恰当。

原理

关注序列的季节周期性，我们的问题是：如何分离序列的 Trend 、Seasonal 和 Residual？换言之，这是关于如何平滑 (Smoothing) 信号的问题。STL (Seasonal and Trend decomposition using Loess, 使用 Loess 的季节性和趋势分离方法) 是一个很琐碎的算法，下文我们对其流程做简述，主要来自原论文。

滑动窗口

考虑一个均值滑动窗口 (Simple Moving Average)，在一定的窗口大小上对窗口内的数据取均值，也即

{\begin{aligned}{\textit {SMA}}_{q}&={\frac {p_{n-q}+p_{n-q+1}+\cdots +p_{n+q}}{2q+1}}\\&={\frac {1}{2q+1}}\sum _{i=n-q}^{n+q}p_{i}\end{aligned}}

熟悉这一概念的读者会立即想到这是滑动窗口算法/卷积/低通滤波/一维的ConvLayer；不约而同地，我们发现简单的滑动窗口

  • 无法更重视更近的数据点

  • 无法排除离群值

考虑改进：

指数加权滑动窗口

S_t = \alpha X_t + (1 - \alpha) S_{t-1}

其中：

-X_t 是时刻t 的原始数据值

-\alpha 是平滑因子，取值范围为0 < \alpha \leq 1

-S_{t-1} 是时刻t-1 的平滑值

特点

-\alpha 越大，当前数据点的权重越高，滤波对突变的响应越快；

-\alpha 越小，历史数据的权重越高，滤波效果越平滑。

LOESS*

局部估计散点图平滑 LOESS (locally estimated scatterplot smoothing) 在序列 {x_n} 上对目标点 x 执行

  1. 赋权

    1. 从近到远排，考虑离 x 第 q 近的点以内的 x_1 \sim x_q

    2. 为这些点赋予权重 \displaystyle v_i(x) = W\left(\frac{|x-x_i|}{|x-x_q|}\right)，其中 W(x) 是某个函数；STL 方法将它设定为 (1-u^3)^3(请特别记住这个 v_i(x)，留待后用)

    3. 上面没有考虑 q>n 的情形；此时，应当令“窗口内的最大距离“ |x-x_q| 修正为 \displaystyle\frac{q}{n}|x-x_n|

  2. 拟合

    1. 考虑对 x_i 点的 d 阶多项式展开 \mu(x) = \beta_0 + \beta_1 (x-x_i) + \cdots + \beta_d (x-x_d)^d (一般把 d 取得很小，文章中取 1 到 2，Python 实现中则取 0 到 1)

    2. 对 2q+1 个窗口内的点，调整参数 \{\beta_n\} 以最小化 {\displaystyle \sum _{i=1}^{2q+1}v_{i}(x)\left(Y_{i}-\mu(x)\right)^{2}.}

    3. 最终，\beta_0 就是对 x 的估计值

总之，上面我们要决定的超参是 q 和 d，实现了连续化和更重视更近的数据点

STL*

STL (Seasonal and Trend decomposition using Loess) 分内外两循环：

  • 内循环更新 S_t 和 T_t

  • 外循环更新稳健权重 \rho_i

外循环

为了避免读者头晕在复杂的细节中，我们先观察外循环：

考虑上一次内循环得到的 S_t^k 和 T_t^k和由此得到的 Residual R_v = Y_v-S_v-T_v，我们定义一个稳健权重 \rho_v = B(|R_v|/h), 其中

  • h 是 6 倍 R_v 的绝对值的中位数

  • B(x)=(1-x^2)^2

并将 \rho_v 乘在当前的 v_i(x) 上，注意到 Residual 很大会导致”稳健权重“很小，所以这个部分为的是 排除离群点

内循环

  • 去趋势 (Detrending)：计算离散的去 Trend 序列： Y_v - T_v^{(k)}

  • 周期子序列平滑 (Cycle-subseries Smoothing) ：对每个周期子序列应用 LOESS，参数为q = n_{(s)} 和d = 1，并扩展至首尾各n_{(p)} 个位置，生成临时 SeasonalC_v^{(k+1)}，范围v = -n_{(p)} + 1 到N + n_{(p)}

  • 平滑周期子序列的低通滤波 (Low-Pass Filtering) 对C_v^{(k+1)} 依次应用：

    • 长度为n_{(p)} 的 SMA（两次）；

    • 长度为 3 的 SMA；

    • 参数为d = 1 和q = n_{(l)} 的 LOESS

  • 输出L_v^{(k+1)}（范围v = 1 到N）

  • 平滑周期子序列的去趋势 (Detrending of Smoothed Cycle-Subseries) ：计算 Seasonal： S_v^{(k+1)} = C_v^{(k+1)} - L_v^{(k+1)}

  • 去季节化 (Deseasonalizing)：计算离散的去季节化序列： Y_v - S_v^{(k+1)}

  • 趋势平滑 (Trend Smoothing)：对去季节化序列应用 LOESS 平滑，参数为q = n_{(t)}和d = 1得到 TrendT_v^{(k+1)}

STL 中有 6 个超参可供调整。

实现

STL

from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(data, model='additive', period=12)

参数：

  1. x，必选

  2. model，additive 或 multiplicative

  3. period，在 x 不是一个 Pandas object 或者 x_index 不具备可见的周期性时必须指明

返回：

  1. result.trend, result.seasonal, result.resid

滑窗

  1. 中心化均值移动平均 data.rolling(window=window_size, center=True).mean()

  2. 指数加权移动平均 data.ewm(alpha=alpha).mean()

附录

Fig.1 的绘图过程：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from matplotlib.dates import YearLocator, DateFormatter

# 设置整体风格
plt.style.use('seaborn-v0_8-whitegrid')

# 导入数据
data = pd.read_csv("./AirPassengers.csv")

# 将 Month 列转换为日期格式并设置为索引
data['Month'] = pd.to_datetime(data['Month'])
data = data.set_index('Month')

# Graph 基础设置
fig = plt.figure(figsize=(8, 10), facecolor='#f9f9f9')
color1 = '#7ca3b8'
color2 = '#ce8a8d'
color3 = '#bfb8d6'
color4 = '#fccb8e'
background_color = '#f9f9f9'

# 分解
decomposition_add = seasonal_decompose(data, model='additive', period=12)
decomposition_mul = seasonal_decompose(data, model='multiplicative', period=12)

# 原始时间序列
ax0 = plt.subplot(4, 1, 1)
ax0.plot(data, color=color1, linewidth=1.5, marker='o', markersize=2, alpha=0.7)
ax0.set_title('Original', fontweight='bold', pad=15)
ax0.set_facecolor(background_color)
ax0.grid(True, linestyle='--', alpha=0.7)
# 横轴 ticks 的设置
ax0.xaxis.set_major_locator(YearLocator(2))
ax0.xaxis.set_major_formatter(DateFormatter('%Y'))
ax0.tick_params(axis='x', rotation=45)

def subplot_setting(data, location:tuple, color:str, title:str, show_xlabel:bool=False, show_markers:bool=False) -> None:
    h, w, index = location
    ax = plt.subplot(h, w, index)
    if show_markers:
        ax.plot(data, color=color, linewidth=1.5, alpha=0.9, marker='.', markersize=3)
    else:
        ax.plot(data, color=color, linewidth=1.5, alpha=0.9)
    ax.set_title(title)
    ax.set_facecolor(background_color)
    ax.grid(True, linestyle='--', alpha=0.7)
    ax.xaxis.set_major_locator(YearLocator(2))
    ax.xaxis.set_major_formatter(DateFormatter('%Y'))
    if show_xlabel:
        ax.set_xlabel('Year')
        ax.tick_params(axis='x', rotation=45)
    else:
        ax.set_xticklabels([])

subplot_setting(decomposition_add.trend, (4, 2, 3), color2, 'Trend/+')
subplot_setting(decomposition_mul.trend, (4, 2, 4), color2, 'Trend/*')
subplot_setting(decomposition_add.seasonal, (4, 2, 5), color3, 'Seasonal/+')
subplot_setting(decomposition_mul.seasonal, (4, 2, 6), color3, 'Seasonal/*')
subplot_setting(decomposition_add.resid, (4, 2, 7), color4, 'Residual/+', True, True)
subplot_setting(decomposition_mul.resid, (4, 2, 8), color4, 'Residual/*', True, True)

plt.tight_layout()
plt.subplots_adjust(top=0.92)
plt.savefig(fname='Figure_1', dpi=300)
plt.show()

Fig.2 的绘图过程：

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose

X = np.arange(1, 51)
y = 10 + X + 10 * np.sin(X * (0.25*np.pi)) + np.random.normal(loc=0, scale=1, size=len(X))

data = pd.DataFrame({'X': X, 'y': y})
data = data.set_index('X')
result = seasonal_decompose(data, model='multiplicative', period=8)

color1 = '#7ca3b8'
color2 = '#ce8a8d'
color3 = '#bfb8d6'
color4 = '#fccb8e'
background_color = '#f9f9f9'
plt.style.use('seaborn-v0_8-whitegrid')
plt.figure(figsize=(16, 4), facecolor=background_color)

plt.subplot(1, 4, 1)
plt.plot(X, y, color=color1, linewidth=1.5, marker='o', markersize=2, alpha=0.7)
plt.title('Original', fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.7)
plt.subplot(1, 4, 2)
plt.plot(X, result.trend, color=color2, linewidth=1.5, alpha=0.9, marker='.', markersize=3)
plt.title('Trend', fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.7)
plt.subplot(1, 4, 3)
plt.plot(X, result.seasonal, color=color3, linewidth=1.5, alpha=0.9, marker='.', markersize=3)
plt.title('Seasonal', fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.7)
plt.subplot(1, 4, 4)
plt.plot(X, result.resid, color=color4, linewidth=1.5, alpha=0.9, marker='.', markersize=3)
plt.title('Residual', fontweight='bold')
plt.grid(True, linestyle='--', alpha=0.7)

plt.savefig('Figure_2.png', dpi=300)
plt.show()

本文参照了以下文献：

  1. Cleveland, Robert B., William S. Cleveland, and Irma Terpenning. "STL: A Seasonal-Trend Decomposition Procedure Based on Loess." Journal of Official Statistics 6, no. 1 (03, 1990): 3. https://www.proquest.com/scholarly-journals/stl-seasonal-trend-decomposition-procedure-based/docview/1266805989/se-2.

时间序列分析 - 滑动窗口和 STL 分解
http://localhost:8090/archives/17dhKTo2
作者
酱紫瑞
发布于
更新于
许可协议
#data-science #时间序列分析