Deep Learning IV - Batch Norm, ResNet, 过拟合的 tricks 和多分类问题
这是 2025 春 计算机视觉导论的笔记
Todo:
- 内容杂乱无章,十分愚蠢,或许未来会润色语言使它便于阅读
Underfitting
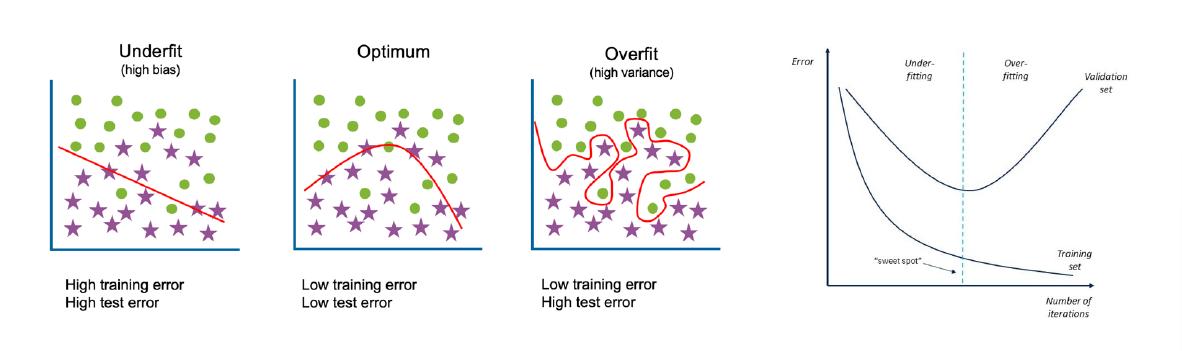
- Underfitting
- 模型在training set上都不好
- 原因:注意dataloader很容易有bug,别搞
X.shuffle,Y.shuffle这种事情 - 原因:模型capacity太小 => 加宽/加深,加深比较有效因为non-linear层是capacity的关键
- Batch Normalization:一般插在 FC/Conv Layer 和 non-linear 之间
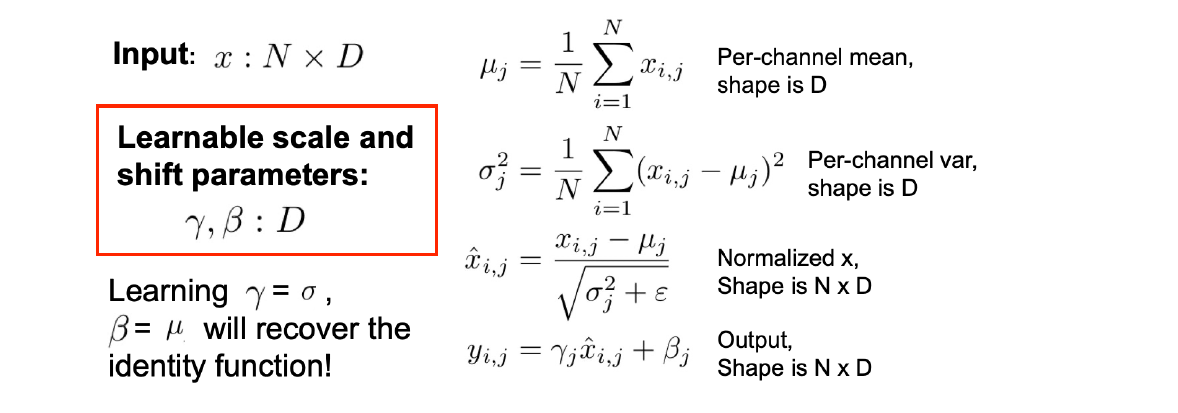
- Training Mode
- 计算每一个输入 batch 的mean \displaystyle \mu和std \displaystyle \sigma
- 进行normalization完成batch的白化/白噪声化/标准正态分布化
- 这大大限制了神经网络的capacity,例如这下ReLU必须砍掉一半了 => 所以存储了参数\displaystyle \gamma和\displaystyle \beta,这是存储在Layer内的param被所有data所共用 => 允许这个Layer去学一个合适的mean和std去干掉指定比例/位置的data
- 结果经过 BN Layer 的一定是一个高斯分布
- Eval Mode (Test)
- 这时明显不能一个个batch地操作了,我们 BN 的mean和std从哪来?
- Eval Mode使用的 \displaystyle \mu 和 \displaystyle \sigma 是训练过程中存储下来的average;相对来说反映了这一个layer需要的mean和std
- Pros and Cons
- 原先每个层只有iteration视角weight \displaystyle W(\displaystyle \omega和bias) -> non-linear,现在还加上了mean和std从整体视角控制data的分布,为layer增加了「自由度更低的 => 因而更美好的可控性」(Personal)
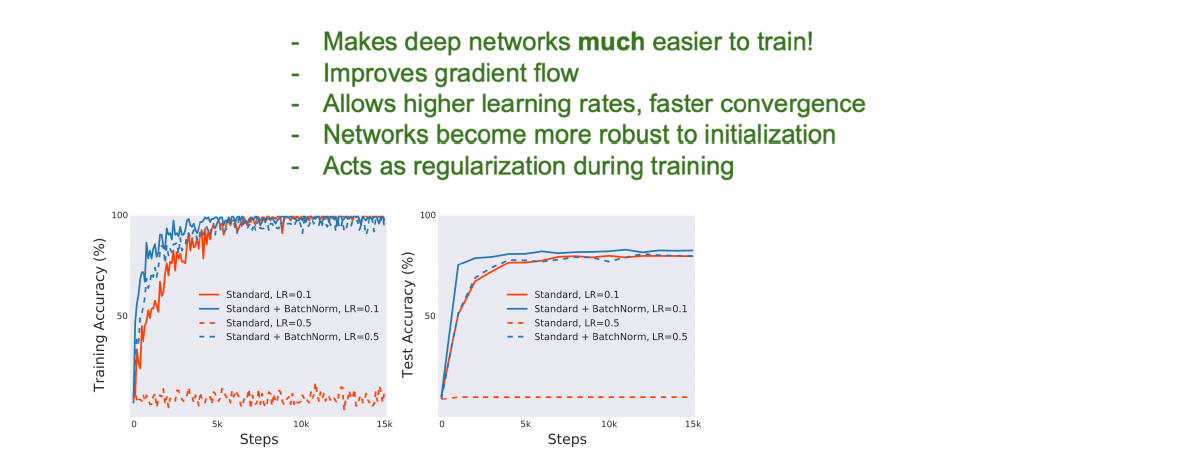 => 对各种各样的数据归到同一的分布从而具有同一的效果,增强泛化能力
=> 对各种各样的数据归到同一的分布从而具有同一的效果,增强泛化能力 - 对更大的LR和更深的layer都有了更好的tolerance,否则high learning rate一下就炸了
- Why?
- Original Hypothsis: mitigate the "internal covariate shift"
- New findings: smoothen the loss landscape (Lecturer: 还行,但不那么清楚)
- Cons
- Train 和 Eval Mode 下对同一个 Data 能产生不同的 output
- batch size越小这种不稳定性越显著 (越大的size的mean和std和总体mean和std越无偏地接近),Test Performance会有一个很大的drop
- 原先每个层只有iteration视角weight \displaystyle W(\displaystyle \omega和bias) -> non-linear,现在还加上了mean和std从整体视角控制data的分布,为layer增加了「自由度更低的 => 因而更美好的可控性」(Personal)
- Normalization Techniques
- 按照Channel数,BatchNorm的mean和std都是 \displaystyle C 维的
- 保持batch内的data point独立性 => 干脆对一个data point的一个Layer求mean和std
- Batch Norm: 跨越data point做norm,一次一个channel
Layer Norm: 一个data point的所有东西做一次norm => 适用于NLP
Instance Norm: 一个图的一个channel做一次norm(不太讲道理,一个Channel的所有pixel的分布怪怪的) => 适用于Style
Group Norm: 一个图,允许沿着channel算,但不允许只算一个channel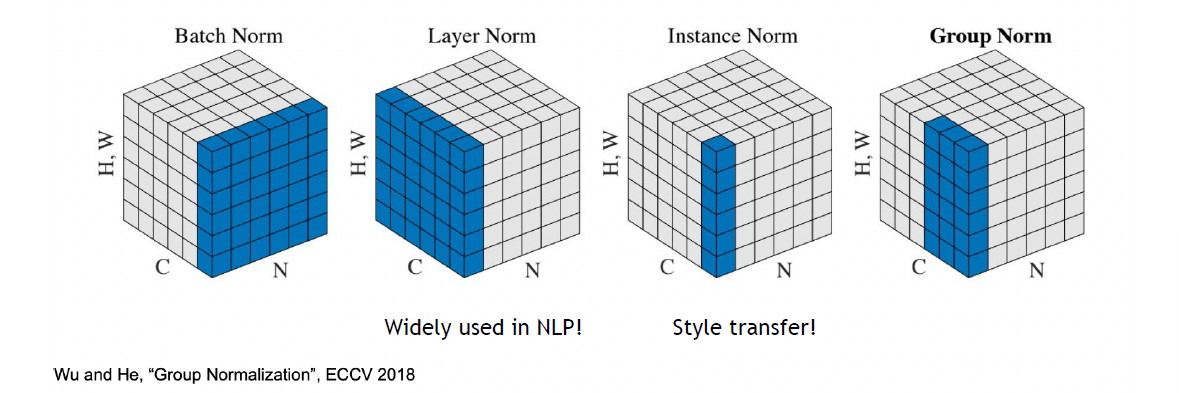 N: 一个batch里的n个data point
N: 一个batch里的n个data point
C: 一个image的c个channel
H, W: flatten的image pixel - 后三种都没有Training/Eval Gap;Layer和Instance对一般任务效果都不太好;batch size小的时候Group Norm效果好于Batch Norm
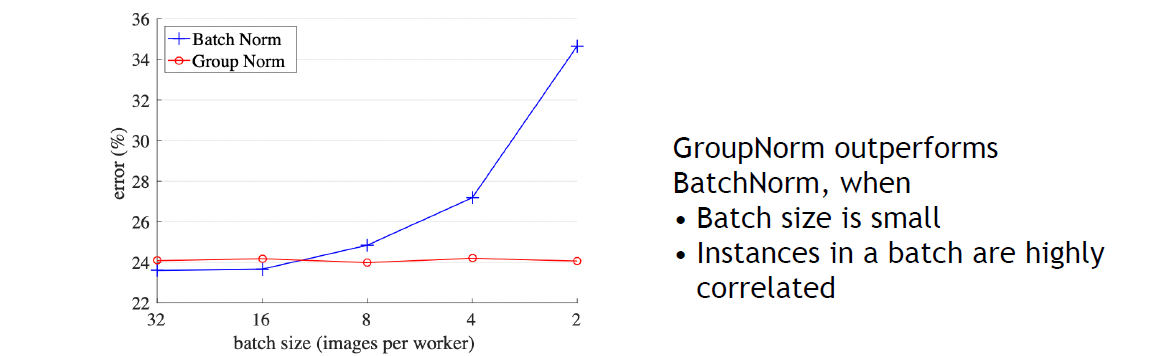
- Training Mode
回顾:
- He Initialization:对激活函数是ReLU的neuron,假设初始数据符合标准高斯分布,让随机化权重乘以 \displaystyle \sqrt{ \frac{2}{\text{Din}} } 使得没有 Covariance shift
- 问题:Loss开始BP以后,W变化,distribution也变化,不再满足高斯分布,仍然容易梯度消失 => 引入 Batch Norm 让每一层都变成标准正态分布
- 问题:每层都是白噪音,capacity不够了 => 引入learnable参数调整分布 (所以初始化为 \displaystyle (0,1) )
- Batch Norm:使Optimization大大容易了
- 问题:输出取决于和我一起进Batch的是什么人/TrainMode和EvalMode Loss有很大的差别,但历史证明BatchNorm就是很有用 => 最大的问题就是按照Batch求mean和std
ResNet
- Problems when CNN gets really deep
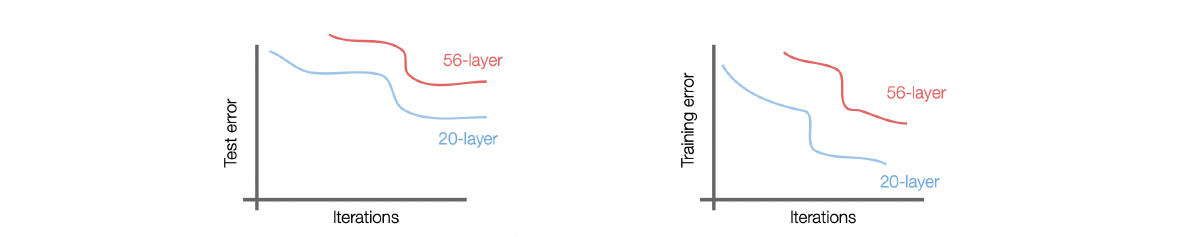
56-layer training error更高可以理解:layer越高就越难拟合;test error更高不能理解:说明并非过拟合的问题!我们认为这是一个optimization的问题:deeper model更难优化 - Fact: 30-layer的Conv+relu甚至学不出\displaystyle H(x)=x,证明后加的层数甚至是有害的:梯度消失 gradient vanishing
- Solution: Residual Block/Skip Link
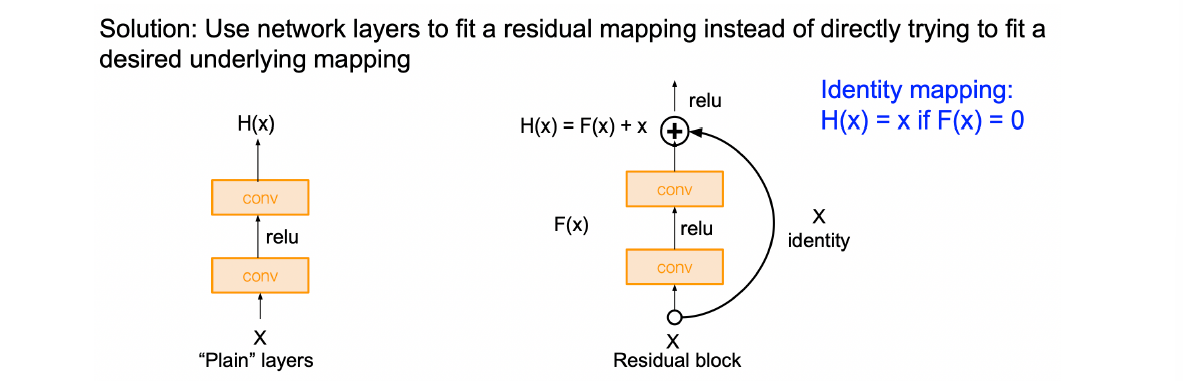
- 从干坏事的角度来说,相当于更深的layer只学习residual,非常棒地实现了类似Taylor展开中逐项逼近的效果;最差的情况下学到的Residual=0(根据ReLU可以想到这是很容易的),至少无害;
- 从BP的角度来说,deep layer的gradient也更容易让shallow的neuron update
- Loss Landscape的解释

Lecturer
我们已经学了何凯明的 He Initialization, Group Normalization 和 ResNet;更多地我们关注的是模型的每一个细节,很多时候是细节上的trick带来模型的跨越性的提升(而不是蓝翔性的调参/训练工作),应该说He的简洁而美好的成果来源于对模型良好的理解
Overfitting
- Early Stopping

|----------Train----------|--Val--|--Test--|:作业/模拟考/高考,在规范的benchmark/challenge上val和test应该同分布,test不应该公布;不应该让模型接触val- 但不能结构上减少train和val之间的gap
- 思路:降低模型的capacity/提高data的diversity
- Data Diversity
- Simply collect more data (expensive & time-consuming)
- Data augmentation 数据增广 (free & fast)
- 简单地transform image
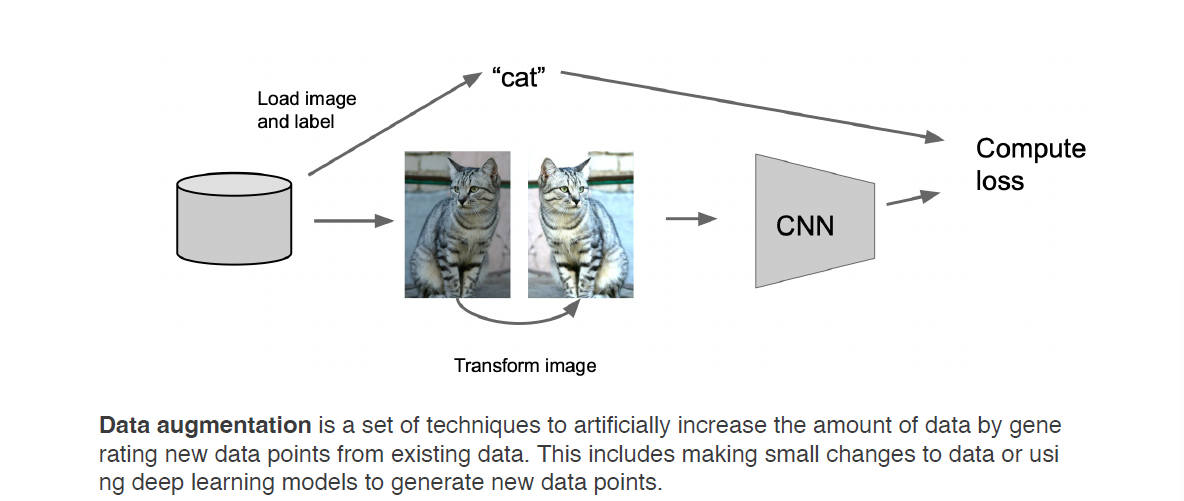
- Horizontal Flip...

- Pros: dataset更难了/提高generalization ability/减少overfitting/creat variability/减少class imbalance
- Cons: magnitude of DA cannot be too strong

Check: 例如手动sample一百个augmentation去人眼看看是否正确
- 简单地transform image
- Regularization
- 限制模型的表达能力:结构上可以让模型更浅;还能添加weight regularization惩罚太大的weight,让loss prefer更简单的模型

- L2 Regularization \displaystyle w^{2}
- L1 Regularization \displaystyle |w|
- 很重要的问题:weight regularization是平方和还是平方和的平均?注意平方和会让regularization太大以至于让data loss忽略不计,这就很不好了,干脆给你学出一个全0的weight
=> 建议:可以在学习的初始阶段先不加,学好后再加loss;仔细调这个超参lambda
- 限制模型的表达能力:结构上可以让模型更浅;还能添加weight regularization惩罚太大的weight,让loss prefer更简单的模型
- Dropout
- 随机把(例如)一半的neuron值设为0
- 原理:让模型对主要特征更加robust

- 结果BatchNorm也有regularization的效果 (follow Gaussian distribution -> limit capacity -> 帮助overfitting,通过帮助optimization帮助underfitting) => 可以减弱overfitting;或许有了BN我们不再需要dropout
结语
- Principle: balance data variability & model capacity (解释: 欠定方程/过定方程)
- Techniques
- (always good) Data augmentation
- (always good) BatchNorm
- Regularization
- (only FC layers) Dropout
- 我们原来说data points的数目应该等于param数,但是或许这也不成立因为每一个neuron都是非线性的(capacity会比线性高)
- No BN at the last layer
- 在最后分类结果上它不应该是单峰高斯分布,不许给我加BatchNorm(!
- example structure:
[(Conv-BN-ReLU)*N-?Pool]*M-(FC-BN-ReLU)*K-FC-SoftMax
Classification
接下来详细来说多分类问题
- Image Classification
- one-hot vector: Ground Truth应该是一个one-hot vector (只有一个维度是1其他都是0)
- 过去的方法
- Nearest Neighbor Classifier
- 假设有一个神奇的Distance Metric func可以衡量不同图片之间的语义距离 (那多分类就很简单了)
- 恐怕难找到这样的函数,无论L1 distance; L2 distance还是其他的东西
- K-Nearest Neighbors (KNN)
- take majority vote from K closest points (所以nearest neighbor就是k=1的情况)
- 问题:首先是distance metric不好说,其次每次得到一个结果要dataset全过一遍这相当吓人
- Nearest Neighbor Classifier
SoftMax
- 前面binary classification我们简单地给输入映了一个sigmoid,现在的任务中我们的目的是得到一个尽可能逼近one-hot vector的结果
- SoftMax Function: given \displaystyle s_{i}=f(x_{i},W), let P(Y=k|X=x_{i})=\frac{e^{ \beta s_{k} }}{\sum_{j}e^{ \beta s_{j} }}

- 初步符合要求
- 加一块是1
- 值在 \displaystyle [0,1] 之间
- 问题:他和 \displaystyle \text{argmax}\left(\begin{bmatrix}s_{1} \\ s_{2} \\ \vdots \\ s_{i} \\ \vdots \\ s_{n}\end{bmatrix}\right) 有什么区别?
- 分析:如果某一维比较大,它的值会被指数函数放大很多,会趋近于1;\displaystyle \beta 很大的时候Softmax就是argmax,很小的时候就是\displaystyle \frac{1}{n} (\displaystyle \beta=1 by default)
- 好处:非交界处有gradient便于优化
- 问题:怎么算loss?
- 回顾:之前binary阶段我们通过MLE的思路推导了loss=prob (p if ground truth=1); (1-p if ground truth=0)
- 注意其实就是两个vector之间的distance => 我们有很多办法计算distance (要求:\displaystyle [0,1])
- Kullback-Leibler divergence D_{\text{KL}}(P||Q)=\sum_{x \in \mathscr{X}}P(x)\log\left( \frac{P(x)}{Q(x)} \right)
- 性质:>=0, =0 only if P=Q
- 为什么叫divergence而不叫distance?
- 不满足对称性
- 不满足三角不等式
- 事实上KL divergence可以分成两部分
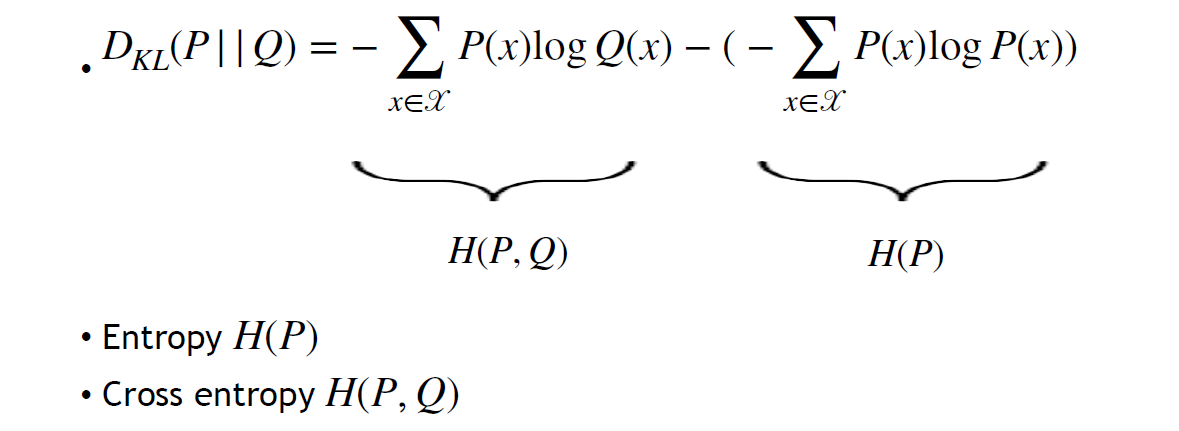
- 如果是one-hot的可以想见混乱度很低熵很小;当然如果ground truth是one-hot的,有0那么必须放在log外面;此时发现H(P)是ground truth的熵(没用) => 引入交叉熵 cross entropy\mathscr{L}_{CE}=H(P,Q)=-\sum_{x\in\mathscr{X}}P(x)\mathrm{log~}Q(x)
- Cross entropy
- 当ground truth是one-hot时cross entropy退化为-log(x_label)
- 随机初始化得到的CE=logn
- 无上限(P=1时Q=0),下限为0
- 其实就是一个NLL(negative log likelihood)
CNN for Image Classification: Brief History
我们关心的事情:
- capacity
- fitness for task
- optimization
- cost
以包含 1000 个 classes,90种狗的ImageNet为例:Top 5 accuracy 2011(75.4%) => CNN(83.6%) => VGG(92.7%) => ResNet(96.4%, 超越人类)
Deep Learning IV - Batch Norm, ResNet, 过拟合的 tricks 和多分类问题
http://localhost:8090/archives/2KIyUxjp