Deep Learning III - Preprocess, Initialization, Optimizer, Learning Rate
这是 2025 春 计算机视觉导论的笔记
Todo:
- 内容杂乱无章,十分愚蠢,或许未来会润色语言使它便于阅读
本节聚焦 Training 的细节和努力减小 Training 和 Test 之间的 Gap
CNN Training
- Mini-batch SGD:For loop
- Sample:Shuffle => Split成batch
(Dataloader) 为什么要Shuffle:为了Random,Dataset可能是按数据类别分类排序的,这样一个batch的gradient会和整个Dataset有很大的偏差 - Forward
- BP
- Update
- Sample:Shuffle => Split成batch
- 框架:TensorFlow❎ => PyTorch & CUDA✅
Data preprocessing
任何操作的目的是 training friendly,但总是 information loss 的
- zero-centered
X -= np.mean(X, axis = 0):为了平等地兼顾各个维
对于图片而言应该是整个dataset求一个所有pixel的mean,也就是说mean是一个(R * G * B)值 - normalize
X /= np.std(X, axis = 0):因为不论是ReLU还是sigmoid都对大于0/小于0最为轻松而敏感;(e.g. VGGNet 不除std,ResNet 除了std)
假想一种红色std很大而蓝色很小的情况,如果对蓝色-mean再/std,这使图片并不显著的蓝色特征(甚至是噪声)被放的特别大(和红色一样了),这显然不利,当然这不是常见的情况;例如对一副蓝色扑克牌的数据集我们就最好不要/std
Weight Initialization
- Small random numbers:
W = 0.01 * np.random.randn(Din, Dout)
~okay for small networks, problem with deeper- 以一个6-layer net为例,每次乘这个Small random W,zero-centered并normalize后的数据分布就向0集中一点

- 意味着gradient dL/dW在layer方向上不断缩小,它们却应用相同的learning rate,所以deeper layer几乎到了all zero的程度,故而no learning
- 如果简单地调大也没有用
 随着deeper,它的gradients也是0. no learning =(
随着deeper,它的gradients也是0. no learning =(
- 以一个6-layer net为例,每次乘这个Small random W,zero-centered并normalize后的数据分布就向0集中一点
- Xavier Initialization:
W = np.random.randn(Din, Dout) / np.sqrt(Din)- 可以保证 Var(y) = Var(x_i) only when Var(w_i) = 1/Din
- 效果:相当于找到了0.01-0.05之间的一个最好的值,使得分布总不会发生变化;起作用的关键并非让每层之间的缩放因子发生变化;这里分布仍然发生了变化是来自tanh的缩放作用

- 解释:\displaystyle \boldsymbol{Y}_{\text{Dout}}=\boldsymbol{W}_{\text{Din, Dout}}\boldsymbol{X}_{\text{Din}},希望如果X~(0, Var),那么Y~(0, Var),因为方差Var(y)=Var(\displaystyle \sum x_{i}w_{i})=Din Var(\displaystyle \boldsymbol{X})Var(\displaystyle \boldsymbol{W}),所以应有 Var(w) = 1/Din
- 对Conv而言?每次运算是把 3 \displaystyle \times 3 个 Cin 变成 Cout,所以 Din = filter_size^2 * input_channels
- Problem: tanh已经过时
- He Initialization:
W = np.random.randn(Din, Dout) / np.sqrt(2/Din)
Change from tanh to ReLU- Xavier 不好用了

- 进行修正:每次乘2
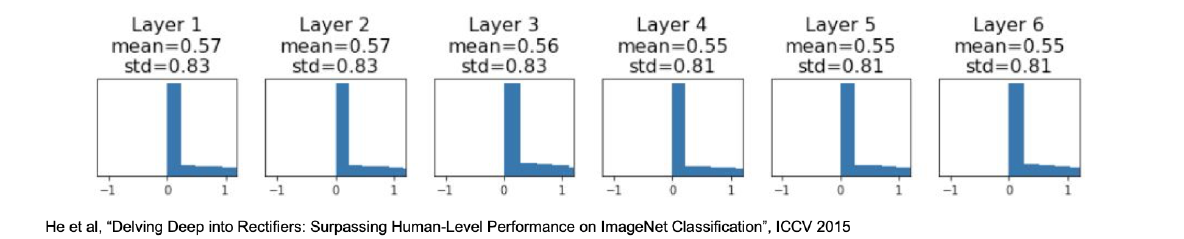
- Xavier 不好用了
Initialization is still an Active Research Area
Optimizer
- SGD Problems
- high condition number: ratio of largest to smallest singular value of the Hessian matrix is large, 疯狂振荡
- 鞍点 saddle point: 它甚至都不是 local minima,但是 gradient 就是0
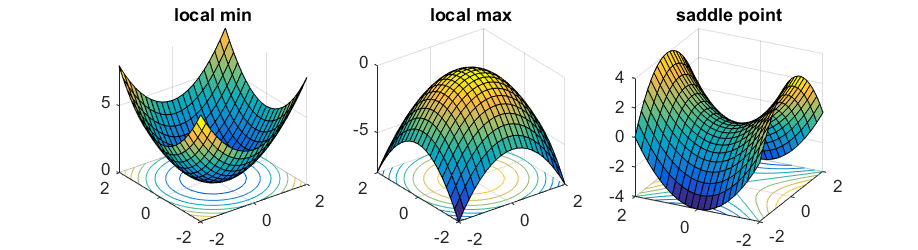 可能表征为loss停留在一个较大的位置不动了
可能表征为loss停留在一个较大的位置不动了 - noisy SGD: 跳出不好的 local minima 和停留在好的 local minima 的冲突
- SGD + Momentum

- Adam

Learning Rate
- Undershoot & Overshoot
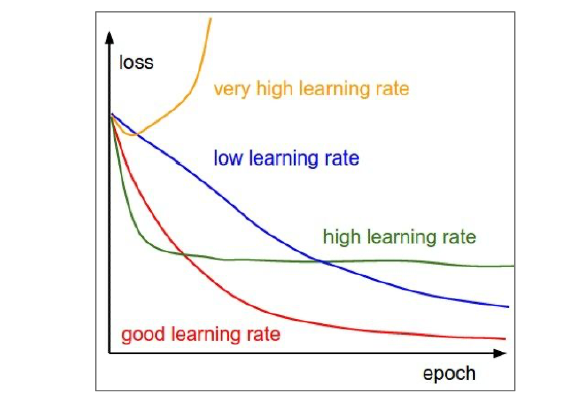
- Appropriate learning rate: 1e-6 ~ 1e-3
- Schedule for learning rate: Step reduce OR Function control
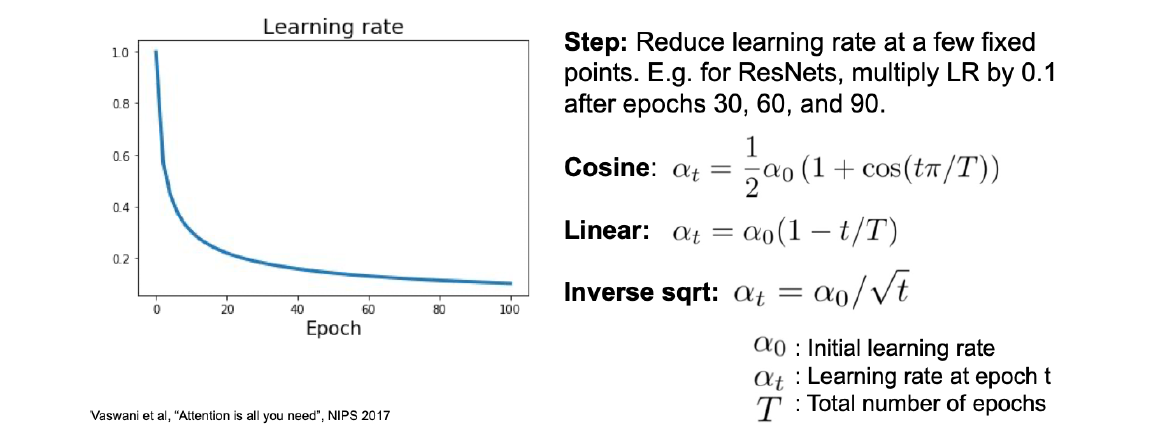
Iteration: \displaystyle W_{t} --- Update Rule --- > \displaystyle W_{t+1}, represents a gradient descent step
Epoch: 对整个training data进行了一整个complete pass是一个epoch
- 可用一个epoch的average loss画loss curve;
- 可以每一整个epoch之后进行一次validation,画plot train curve
- Validation Loss
- e.g. NLL Loss on Validation Dataset
- Evaluation Metric
- Accuracy
- Precision/Recall
- F1
- ...
- 可以每一个epoch后存个档
对于特别大的数据集,真的要一个epoch做一个plot train curve的point,evaluate on val,save model吗?不好;根据具体情况更好,很多llm「一次成型」只训一个epoch;让我们重新定义epoch!认定一个epoch就是5000个iteration,这也好. 只是注意
- 像learning rate schedule这些东西的重新处理;
- 总是要根据dataset的大小调整:如果数据集大小翻了倍?首先epoch的大小是受显存限制的,dz的3050Ti显然就不能照抄人家H100的batch_size()注意模型真正的基础是iteration,调schedule最终应该看根据batch_size缩放;
- 理论上batch size大,gradient质量更好,但噪声也更小,经验公式:learning rate ~ batch size;
- 2倍的iteration数和2倍的batch size哪个更好?这没有的确定答案
Deep Learning III - Preprocess, Initialization, Optimizer, Learning Rate
http://localhost:8090/archives/4WmfFYcJ