这是 2025 春 计算机视觉导论的笔记

Todo:

• 内容杂乱无章，十分愚蠢，或许未来会润色语言使它便于阅读

接上节：线性模型的 capasity/expressivity 太小了！

Multi-Layer Perceptron (MLP)

1. 线性层堆叠没有意义：\displaystyle \mathbb{R}^{c_{1}} \to \mathbb{R}^{c_{2}} \to \mathbb{R}^{c_{3}} 仍然是线性的，堆 non-linear 的东西才有用
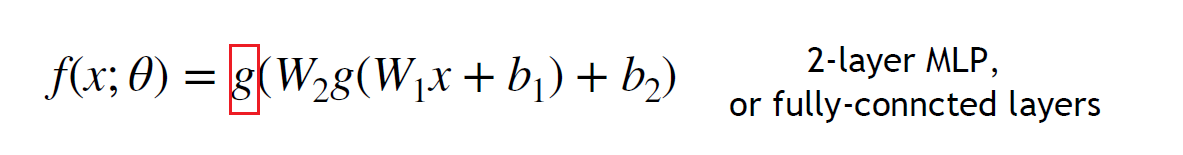
   有意义的 \displaystyle g
   1. 要做的事：Input -> flatten -> Hidden Layer -> Output
   2. fully-connected 全连接层，下一层的所有neuron都连接到上一层的所有neuron
   3. Hidden Layer 的选择：选 Input 和 Output 之间的一个值，或许从信息凝聚的角度解释
2. 范式
   1. Initialization: randomly generate \displaystyle \boldsymbol{W}_{1}\in \mathbb{R}^{784\times 128} and \displaystyle \boldsymbol{W}_{2}\in \mathbb{R}^{128\times 10}
   2. Forwarding(前向传播)
   3. Gradient Descent: Update weights
3. Backpropagation
   1. 我们已经不太好给出多层情况下 Gradient 的解析形式
   2. Chain Rule
      1. Upstream gradient 一步步与中间的 Local Gradient 相乘最后回到第一层
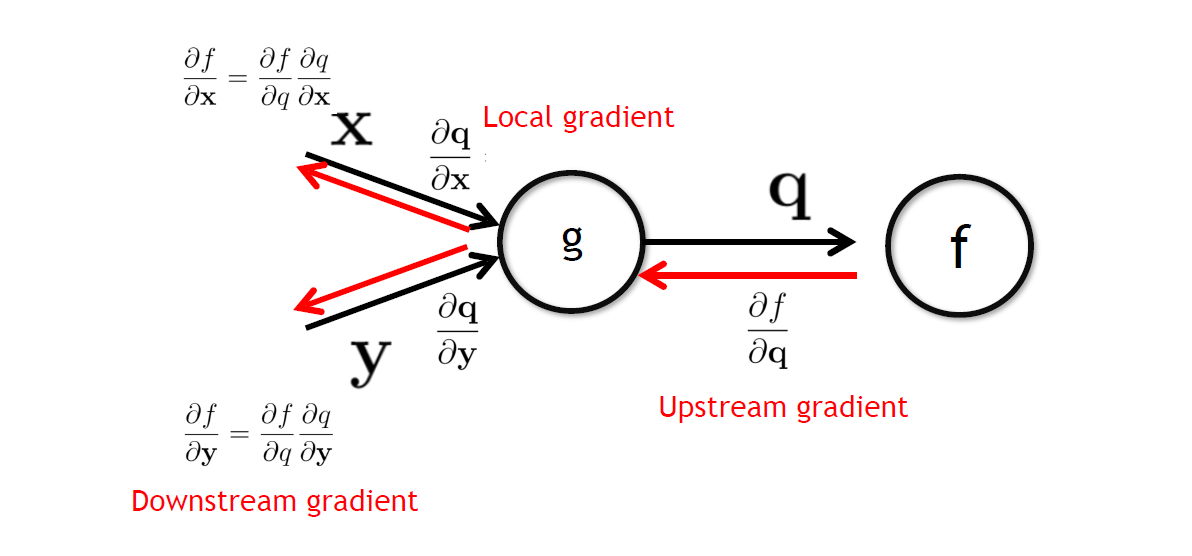
      2. 这样实现了自动微分机制 Auto Differentiation，Computational Graph -> Diff.
4. Activation Function
   1. 之前用到 Sigmoid 是把 \displaystyle \mathbb{R} 映到 \displaystyle [0, 1]
   2. 这里的激活函数是用来实现 non-linear 的 neuron，因为有non-linear，所以有一切函数
   3. 选\displaystyle \tanh？不会丢掉一半区间；选\displaystyle \text{ReLU}？事实上只要不是全线性，就不会退化为一个线性层，这样可以简化计算；
   4. Optimization上，ReLU负位置的前面的neuron在BP时干脆可以直接丢掉了，不被Update；引入Leaky ReLU使得BP时所有neuron都被update
   5. 为什么大家还是愿意使用ReLU？在正位置性质足够好；可以从生理上理解；Rectified Linear Unit
   6. tricky要用到更加好的optimization，比如leaky relu；但是对于分类这样的问题，relu就足够好

结语

• MLP 采用的 Model：Input -> function: Hidden Layer(non-linear) -> Output
• 如何让 function 足够 non-linear：非线性的激活函数的叠加
• MLP 结构 & Chain Rule：Initialization -> Forwarding -> Backpropagation

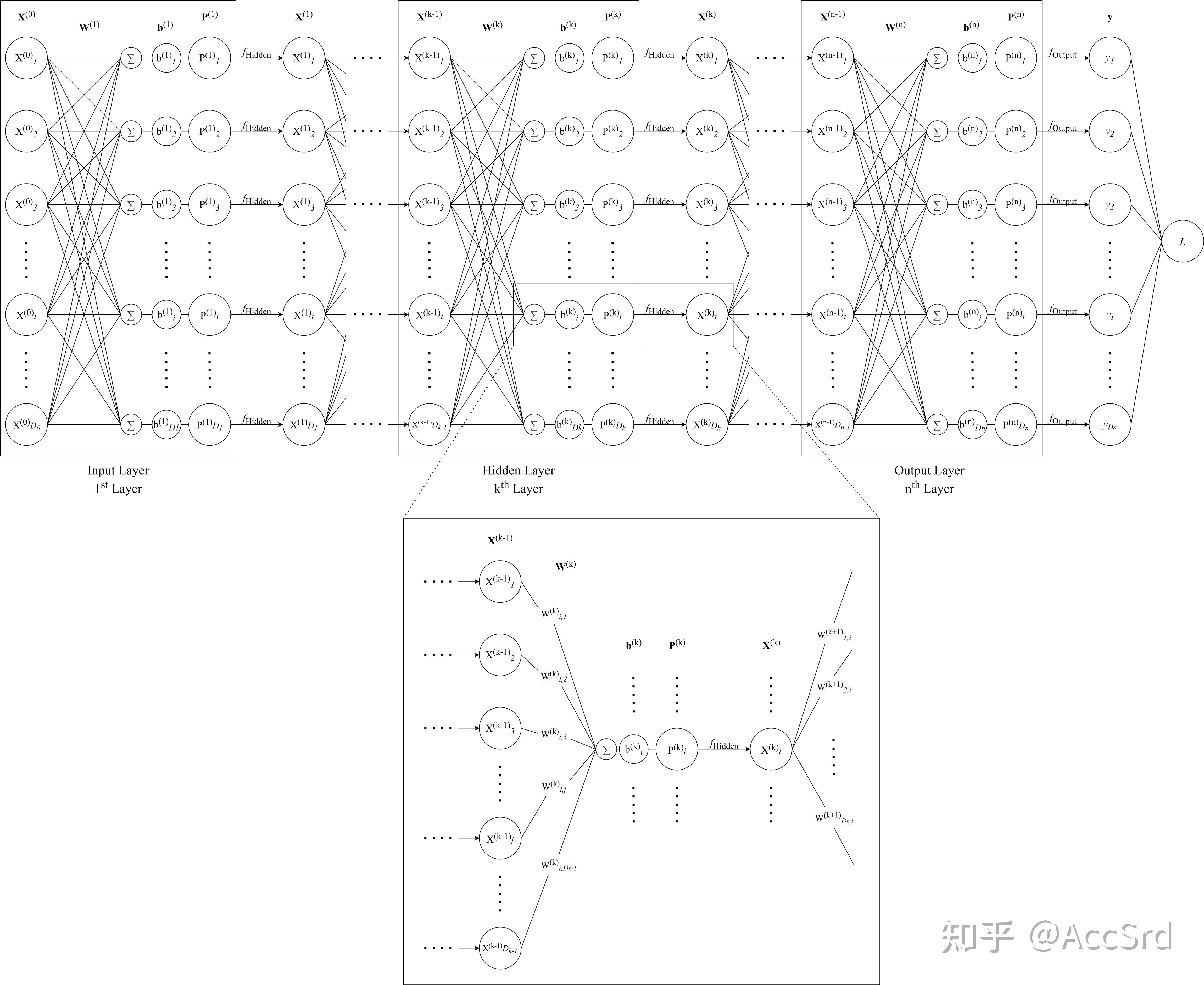
Convolutional Neural Network

1. MLP Problems
   1. Deep Learning I 中学习了 FC 全连接网络
   2. MLP 由多层的 FC 构成，也有人管 MLP 叫 FC
   3. MLP 用最丰富的神经连接相连接的神经层，很贵，适于处理密集的数据；flatten也很不讲道理，破坏了图片的结构；矩阵\displaystyle \boldsymbol{W}也非常巨大，参数量很恐怖
2. CNN

   1. 卷积操作

      1. 卷积核kernal/filter参数通过学习得到(一个convolution kernal应该是C个filter)
      2. 不严格遵循卷积规则：直接对位相乘；但其实仍严格符合数学的卷积定义
      3. 考虑 image(\displaystyle 32\times 32 \times 3) 和 filter(\displaystyle 5 \times 5 \times 3) 之间的点积，最后得到\displaystyle 32 \times 32 \times 1(channel=1)的结果
      4. 这时候filter是否各向同性都无所谓了，与要抽取的特征有关
      5. filter可以再加bias => \displaystyle w^{T}x+b
         1. share1个bias 还是 \displaystyle 32\times 32 \times 3个bias还是 \displaystyle 5\times 5 \times 3个bias？
         2. 结果是共享同一个bias
         3. 其他的选择：不符合Conv的规则，破坏卷积的平移等变性
      6. 角落上的Conv：最原始的大小缩减作用

   2. 可以由多个filter各对image卷积一次，得到一组activation maps/feature maps

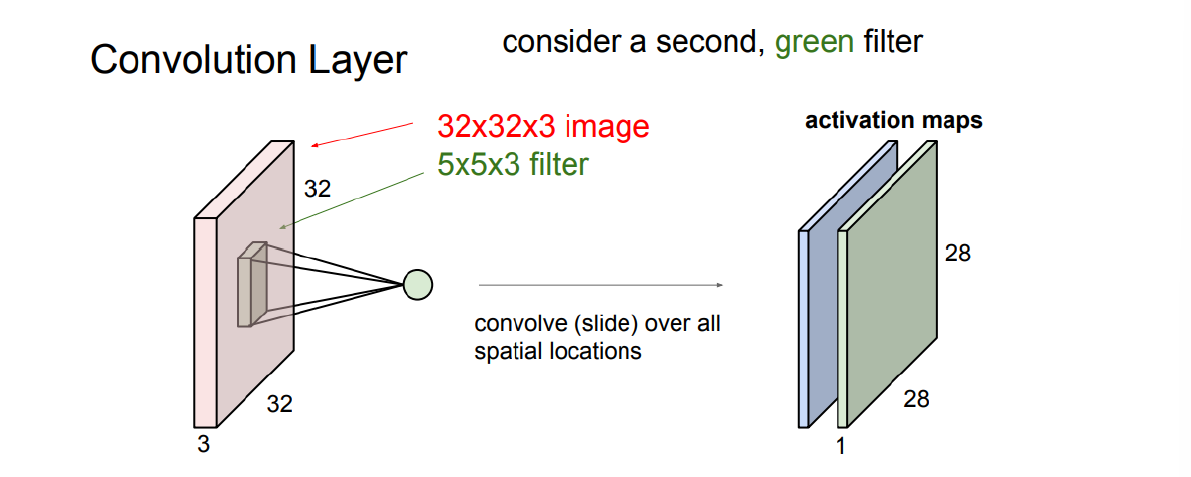
      信息从局部语义向更高维的空间移动

   3. 完成Conv后一定要做ReLU：两次线性操作之间

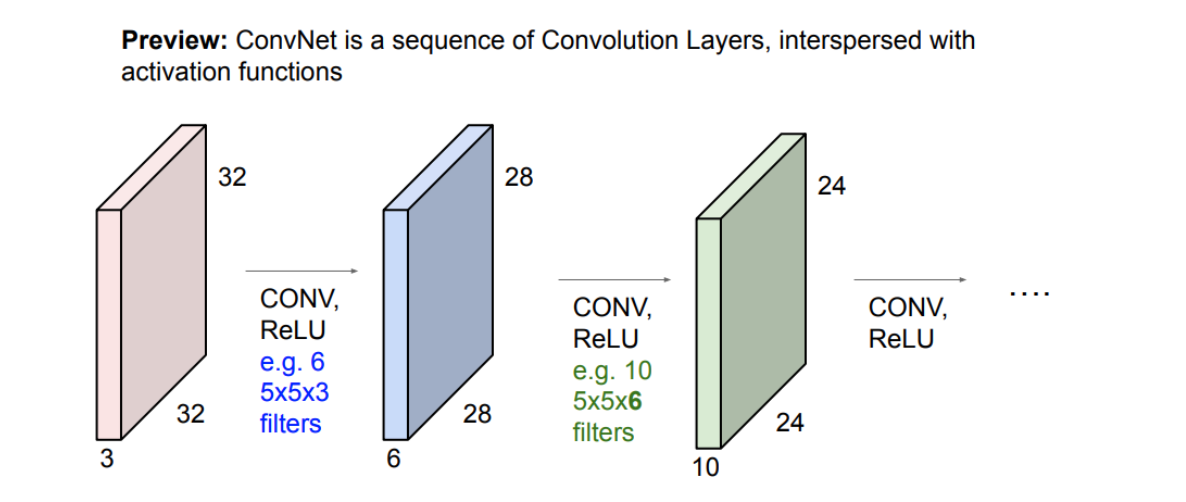
   4. 最后还是用一个Linearly separable classifier(FC)得到结果

      1. ReLU的意义：feature extract，杀掉neuron
      2. bias的意义：决定杀掉哪些neuron
3. 步长 Stride：增强大小缩减作用 => 不匹配时就会损失信息
   1. Output size: (N - F) / stride + 1 => 不匹配就得到非整数
   2. 补救手段：padding
      1. zero
      2. Output size' = (N + 2P - F) / stride + 1, 其中 P = (F - 1) / 2 会实现输入输出dimension不变 (这很好 :P)
   3. parameters number: filter_num * (x * y * channels + 1)
      1. CNN 大大减少了 parameters 数量！
   4. Common Setting：取channel数为powers of 2，filter size是奇数(容易padding)
4. 池化 Pooling
   1. 池化真是莫名其妙的翻译，这是另一种大小缩减方法
   2. e.g. MAX Pooling 在每一个 2 \displaystyle \times 2 filter 里取最大的那个(信息损失还好，因为只要不是第一层Conv，这个 MAX 就是先前周围几块通过filter综合得到的)
      Average Pooling 等价于一个 \displaystyle \begin{matrix}1 & 1 \\ 1 & 1\end{matrix} 的 \displaystyle 2 \times 2 filter, stride = 2
   3. 处理奇数情况：\displaystyle W^{\prime}=\left\lceil \frac{W}{2} \right\rceil
   4. 应用例：Style -> Average Pooling Classification -> MAX Pooling

Comparison

1. FC and ConvLayer
   1. FC: fully/densely connect
   2. ConvLayer: 一个输出cell只和周围filter size内的输入有关，parameters远少于FC => 计算开销
      1. 近场效应 Sparse Connectivity => 信息蔓延的过程 (受到了来自 transformer 的挑战)
      2. Parameter Sharing => 这是Conv与生俱来的
2. FC and CNN: which is more expressive?
   1. FC is super set of CNN: FC 显然可以表达所有的 Conv(只需要non-sparse的神经weight为0)
   2. FC is worse than CNN: MLP 在训练集上的 accuracy 都会不高，更不用说过拟合：在巨大的空间中有过于多的local minima，param太多了
3. 识别猫猫：背景/角度/光照变化太多，网络应该对这些因素具有robust => CNN天然
   例子：
   对FC来说Input翻天覆地了！
4. CNN对transform是Equivariance的：S_{A}[\phi(X)]=\phi(T_{A}(X))
   rotation如果是isometric的那么是equivariance的，但大概率filter不是isometric的，那么rotation可能就没有equivariance，但小的rotation下 Pooling 会对rotation有一定的robust
5. 这 终于！ 特别好地回答了为什么要 parameter sharing
6. 结论：CNN with ConvNet 和 pooling layer 对 translation 很好地 invariance，rotation有一点点invariance；CNN在各处有相似质量的local minima