3D Data

我们把3d representation分成implicit隐式立体和explicit显式立体
implict：例如双目视觉通过双眼视角差产生立体视觉就是隐式3d，并不精确，是相对感知；为什么相对感知能完成生活中的各种任务？老师的解释是人眼在进行连续观测，在伸手的过程中能不断修正
explicit：Depth Cam/LiDAR都是RGB+Depth的，给出显式的精确的深度信息；总之，这样的3d data既有regular data（multi-view的，rgbd的，体素的），也有irregular data（经典的三角面/四边面mesh，点云point cloud）

Camera Model

我们其实在图形学里学过这个：从观察空间到屏幕空间的投影矩阵

建立相机Model的Idea
1. 空气中的一张相纸？不可以，相纸上的每个点会接收到世界上各处射来的所有光，不同来源的光混杂在一起，不能成像
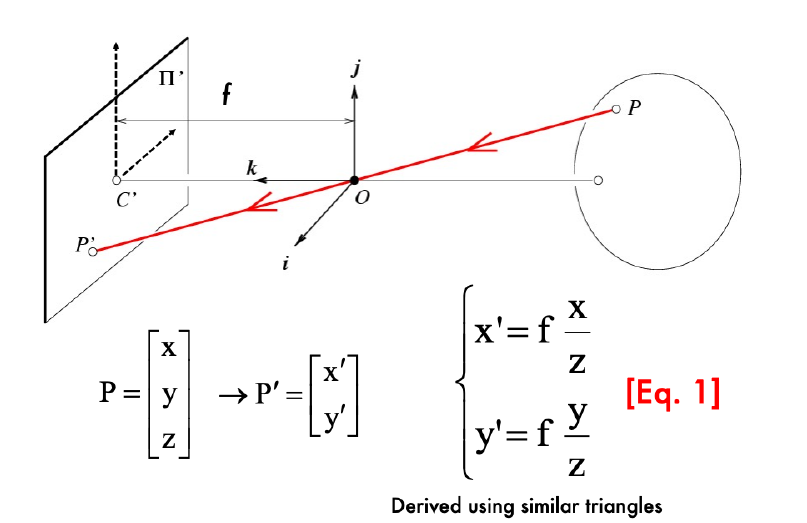
2. Pinhole camera：一个相机模型可以数学化为 $\displaystyle f\left(\begin{bmatrix}x \\ y\end{bmatrix}\right)=\begin{bmatrix}x \\ y \\ z\end{bmatrix}$ ，Pinhole Camera是
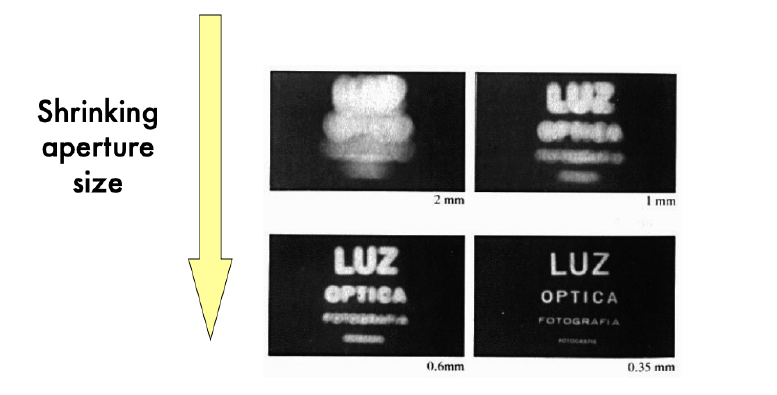
3. Pinhole Cam Cons：只有无限小的小孔能让一个位置的光只来自于一点；减小aperture size又与光度矛盾
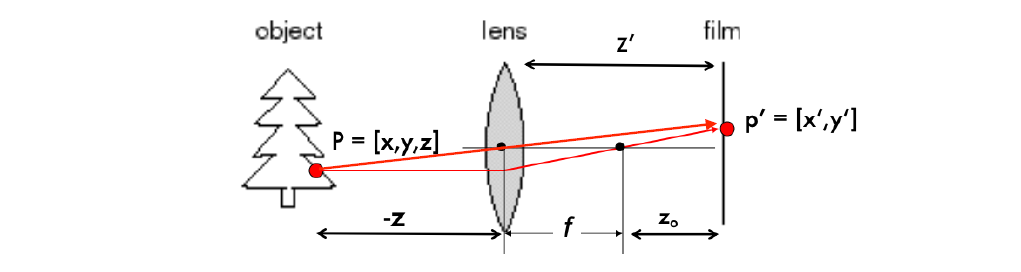
4. Paraxial Refraction Model 近轴折射模型：根据所有平行光通过lense会汇聚在焦点上，物点记作 $\displaystyle [x,y,z]$ ，像点记作 $\displaystyle [x^\prime,y^\prime]$ ，有 $\displaystyle \frac{x^\prime}{z^\prime}=\frac{x}{z}$ , $\displaystyle \frac{y^\prime}{z^\prime}=\frac{y}{z}$
5. 虚焦/桶形畸变
两种相机参数：Intrinsics，相机的内在参数，制造好就不变了；Extrinsics，外在参数，随空间位置和朝向变化

Intrinsics

回顾刚才建立的Model $\displaystyle \left\{ \begin{aligned}x^\prime = f \frac{x}{z} \\ y^\prime = f \frac{y}{z}\end{aligned}\right.$ , 我们一方面令相纸原点为 $\displaystyle (c_{x}, c_{y})$ , 一方面乘上 $\displaystyle (k, l)$ 把量纲化为pixel，并为了方便令 $\displaystyle fk=\alpha, fl=\beta$ ，两个常量的量纲都是 [pixel] 从而得到相机模型 $\displaystyle (x, y, z) \implies \left(\alpha \frac{x}{z}+c_{x}, \beta \frac{y}{z}+c_{y}\right)$ ，这是一个非线性变换，因为存在一个「除以 $z$ 」。我们需要将它表达为矩阵形式，为此，引入齐次坐标(Homogeneous Coordinate)，齐次坐标 $\displaystyle \begin{bmatrix}x \\ y \\ w\end{bmatrix}$ 对于欧几里得坐标 $\displaystyle \left(\frac{x}{w}, \frac{y}{w}\right)$ ，就得到投影矩阵 $\displaystyle P^\prime=\begin{bmatrix}\alpha x+c_{x}z \\ \beta y+c_{y}z \\ z\end{bmatrix}=\begin{bmatrix}\alpha & 0 & c_{x} & 0 \\ 0 & \beta & c_{y} & 0 \\ 0 & 0 & 1 & 0\end{bmatrix}\begin{bmatrix}x \\ y \\ z \\ 1\end{bmatrix}$ , 投影矩阵 $\displaystyle M$ 中除去非0列的 $\displaystyle 3\times 3$ 矩阵 $\displaystyle K$ 蕴含了所有相机的内参信息，投影过程也简化为 $\displaystyle P^\prime = MP=K\begin{bmatrix}I & 0\end{bmatrix}P$

Extrinsics

为什么上面的推导没有任何外参？我们也在图形学中接触了，刚才的投影矩阵 $\displaystyle M$ 是从 观察空间 到屏幕空间的， $\displaystyle (x, y,z)$ 的原点是相机，所以我们只用再引入从 世界空间 到观察空间的变换矩阵就可以了

回顾 $\displaystyle 3\times 3$ 旋转矩阵 $\displaystyle R$ 满足的条件：不含镜像的正交矩阵 $\displaystyle \Leftrightarrow$ $\displaystyle R^\top R=I,\det(R)=+1$ ；观察空间/相机坐标系满足 $\displaystyle \begin{bmatrix}x_{cam} \\ y_{cam} \\ z_{cam}\end{bmatrix}=R\begin{bmatrix}x \\ y \\ z\end{bmatrix}+T$ ，再写成齐次的就是 $\displaystyle \begin{bmatrix}x_{cam} \\ y_{cam} \\ z_{cam} \\ 1\end{bmatrix}=\begin{bmatrix}R_{3\times 3} & T_{3\times 1} \\ 0 & 1\end{bmatrix}\begin{bmatrix}x \\ y \\ z \\ 1\end{bmatrix}$ ，左乘前面Intrinsics的成分即 $\displaystyle P^\prime_{3\times 1}=K_{3\times 3}\begin{bmatrix}R & T\end{bmatrix}_{3\times 4}P_{4\times 1}$ ，得到的齐次坐标转换为欧几里得坐标即可；结果的相机模型是一个从世界空间到屏幕空间的变换矩阵，它保直线，不保平行，近大远小。

如果所有物点都离相机特别远，我们就近似认为 $\displaystyle z$ 是一个常数，此时得到的变换成为Weak Perspective Projection，它是纯线性的（它是一个正交投影？），好算。

（好吧，老师接下来立刻介绍了正交投影）Orthographic正交投影是完全保长度的变换，可以测量物体的真实高度

Camera Calibration

Problem

分析 $\displaystyle K,R,T$ : 合并它们三个是这么一坨东西

M=\left( \begin{array} {cc}\alpha\boldsymbol{r}_1^T-\alpha\cot\theta\boldsymbol{r}_2^T+u_0\boldsymbol{r}_3^T & \alpha t_x-\alpha\cot\theta t_y+u_0t_z \\ \frac{\beta}{\sin\theta}\boldsymbol{r}_2^T+v_0\boldsymbol{r}_3^T & \frac{\beta}{\sin\theta}t_y+v_0t_z \\ \boldsymbol{r}_3^T & t_z \end{array}\right)_{3\times4}

或者关注原始定义

\mathbf{K}= \begin{bmatrix} \alpha & -\alpha\cot\theta & \mathrm{u}_\mathrm{o} \\ 0 & \frac{\beta}{\sin\theta} & \mathrm{v}_\mathrm{o} \\ 0 & 0 & 1 \end{bmatrix}\quad\mathbf{R}= \begin{bmatrix} \mathbf{r}_1^\mathrm{T} \\ \mathbf{r}_2^\mathrm{T} \\ \mathbf{r}_3^\mathrm{T} \end{bmatrix}\quad\mathbf{T}= \begin{bmatrix} \mathbf{t}_\mathrm{x} \\ \mathbf{t}_\mathrm{y} \\ \mathbf{t}_\mathrm{z} \end{bmatrix}

$\displaystyle T$ 有3个自由度， $\displaystyle R$ 事实上只有3个自由度， $\displaystyle K$ 有 $\displaystyle \alpha$ , $\displaystyle \beta$ , $\displaystyle u_{0}$ , $\displaystyle v_{0}$ , $\displaystyle z$ 5个自由度，求解 $\displaystyle M$ 本质是从图片求解11个变量。我们引入 校准架 (Calibration rig)，认定世界坐标系就是这个校准架。给定了定位点 $\displaystyle P_{1}\dots P_{n}$ ，具有

已知的校准架上的坐标
已知的相片上的坐标

我们至少要让 $\displaystyle n=6$ ，即具有6个correspondences，一个 $\displaystyle P$ 有 $\displaystyle (x,y)$ 可以列 2 个方程，12 个方程求解 12 个变量；一般会取大于 6 的 $\displaystyle n$ 交叉验证。

Solution

=== 推理 ===> 得到所要求解的方程即是 $\displaystyle \boldsymbol{Pm}=0$ , 其中 $\displaystyle \boldsymbol{m}=\begin{bmatrix}m_{1}^\top \\ m_{2}^\top \\ m_{3}^\top\end{bmatrix}_{12 \times 1}$ , 那和以前求解最小二乘法一样，我们可以用 SVD Minimize $\displaystyle |\boldsymbol{Pm}|^2$ , under constraint that $\displaystyle |m|^{2}=1$ 。P SVD 分解为 $\displaystyle UDV^\top$ ，V 的最后一个 column 就会给出 $\displaystyle \boldsymbol{m}$ ，进而得到 $\displaystyle K, R, T$

要注意至少需要两个不平行的棋盘格来求解，这是因为 $\displaystyle K$ 蕴含了 FoV，而你可以注意到单个棋盘格是无法确定 FoV 的，你就知道了 $\displaystyle K$ 求不出。

我们当前的 Calibration 是基于近轴折射模型的，对一个大视场角的相机你必须进行畸变矫正，这超出了本节的范围。

Example

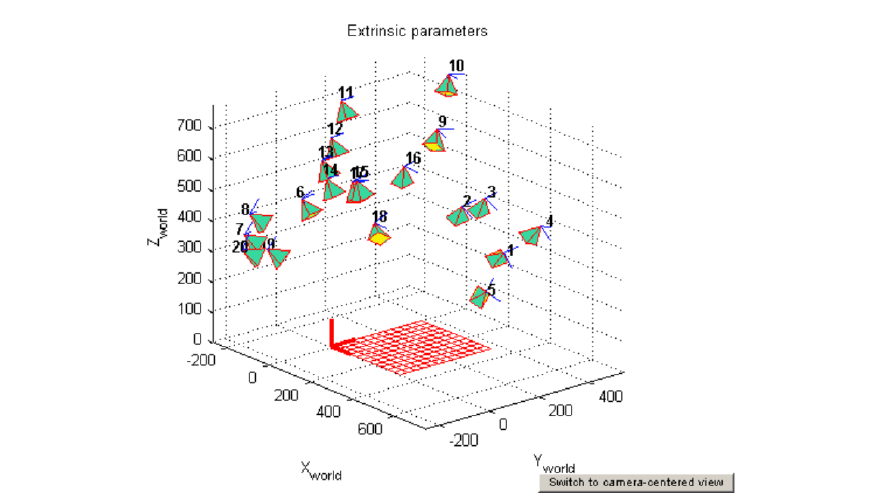
Metrics

给出测试集，包含标注好的3d和2d位置，用预测的3d位置和标注求例如MSE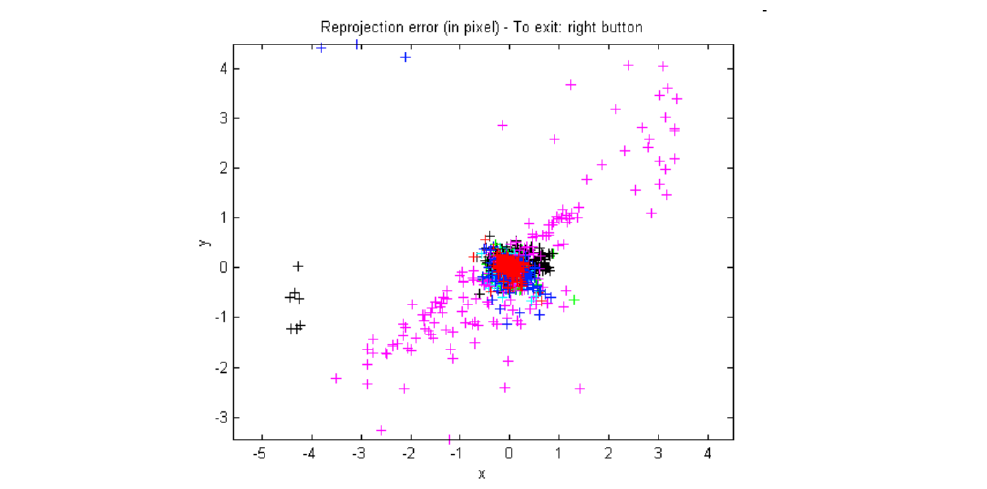

对上面的error，误差很多集中在1个pixel内，这很准了；紫色的棋盘可能...

交叉点标注有问题
更可能是 $\displaystyle R,T$ 有问题，因为 $\displaystyle K$ 是和其他棋盘共享的

Depth Image

Depth 是 $\displaystyle H\times W\times 1$ 的数据，激光雷达给的原始数据是 ray depth（球坐标系），但我们一般谈论的深度图存储的实际上是 z depth（柱坐标系）！

Depth Image必须知道Intrinsics才能转换成 $\displaystyle (x,y,z)$ ，所以并非真正的3D data；当我们把depth image back projection成 $\displaystyle (x,y,z)$ ，才能得到点云。

3D Vision I - 3D Data, Camera Model, Calibration

http://localhost:8090/archives/DgvrVJQh

作者

酱紫瑞

发布于

2025-05-20

更新于

2025-05-20

许可协议

#CV 导论