AR 模型
自回归/Autoregressive model/AR(p) 模型假设当前时刻的值可以表示为过去 p 时刻的线性组合,即{\displaystyle X_{t}=\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t}}
我们接下来将阐述
AR 模型需要序列具有 自相关性
AR 模型需要序列具有 弱平稳性
满足这两点后,我们即可使用 AR 模型进行最终目的:预测。
在下面,我们会学习使用自回归模型进行时间序列分析的一般方法,通过 PACF 确定 AR 模型的 p 值,通过 ADF 检验验证序列的平稳性,采取一些平稳化手段,从而估计各个 \varphi 值,建立 AR 模型进行预测
自相关性
我们想要一致地讨论一个一个时间序列与其自身的滞后版本之间的相关性,第一想法是使用归一化到 [-1, 1] 的协方差衡量,即
称之为自相关系数,将不同的 k 下的自相关系数组成的序列称为 ACF 序列。
ACF
ACF 可以捕捉序列的潜在周期性 再次以 AirPassengers 数据集为例:
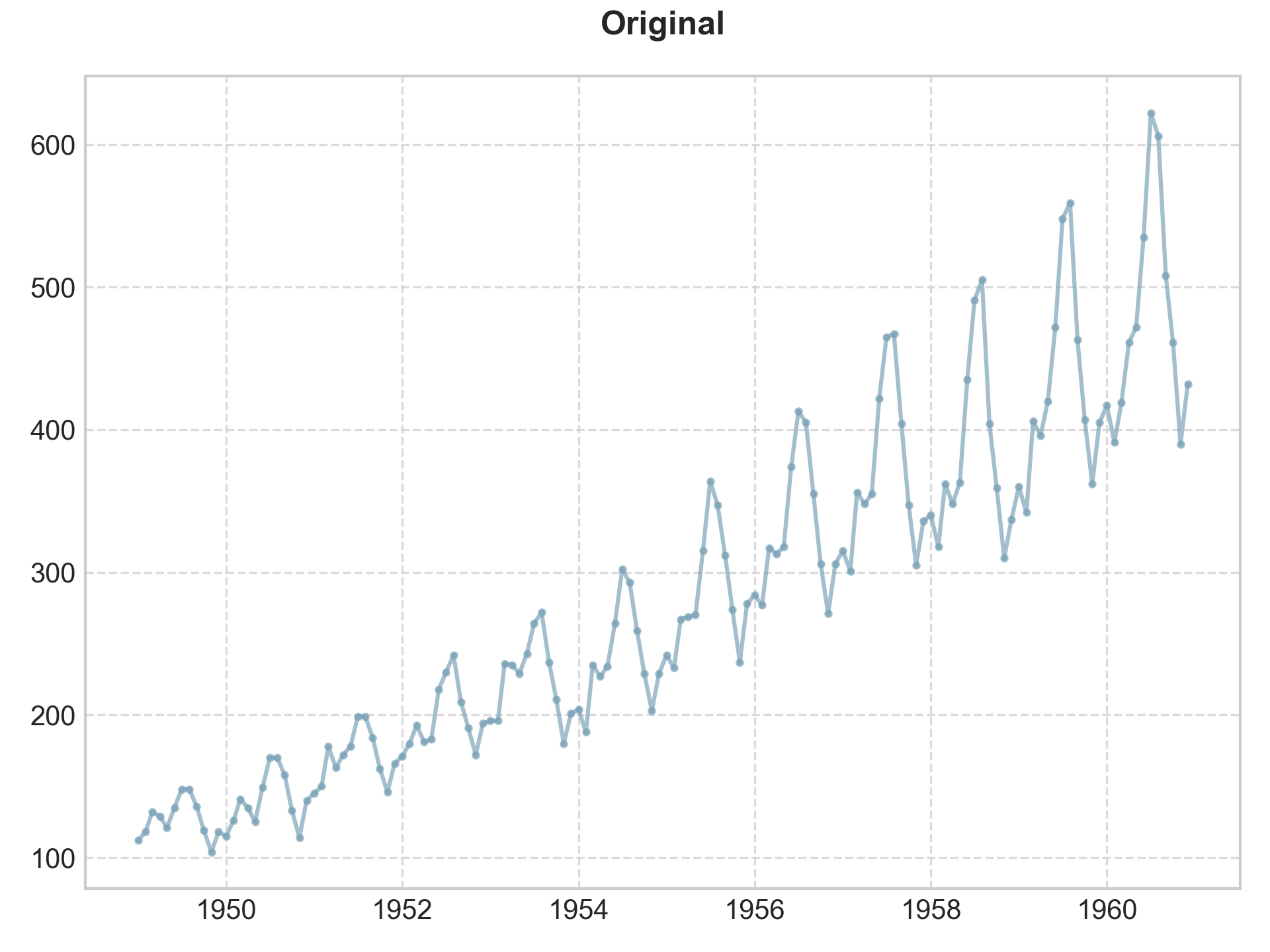
使用 plot_acf() 得到结果:
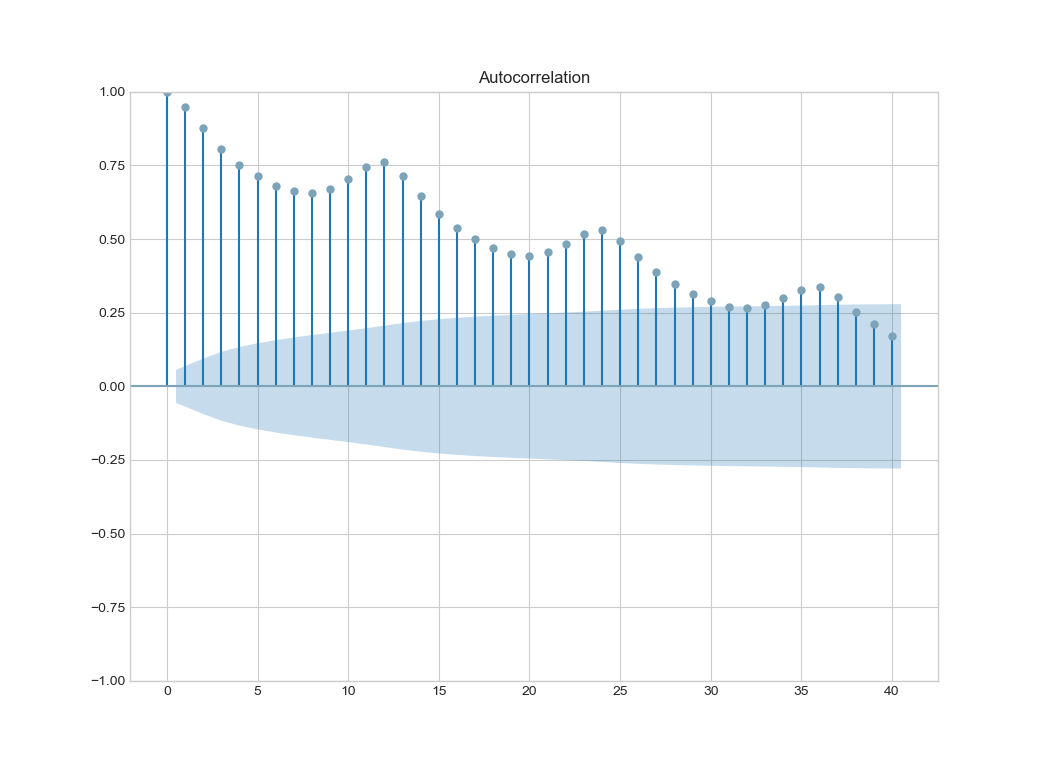
其中,值表示自相关系数,浅蓝色区域是 95% 置信区间;lag=0 时自相关系数毫无疑问是1;我们发现每隔 12 个月序列有一个较强的自相关性,说明序列有季度周期性的现象。
使用 ACF 确定 AR 模型的 p 值 构造一个 AR(1) 模型 y_t = y_{t-1} + \varepsilon 尝试画它的 ACF 图: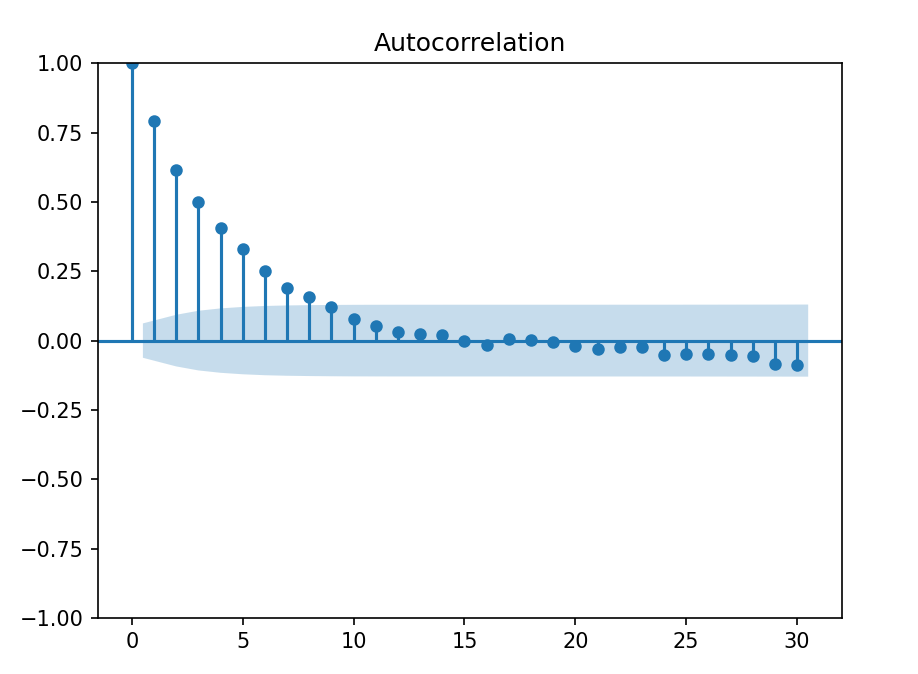
的确没错:自回归系数随 lag 增大指数递减;但问题是我们无法确定一个 p 值,在这个意义上 ACF 不够好。
PACF
上面的问题源于 ACF 捕捉了所有滞后阶数的混合影响,高阶相关性可能完全仅由中介导致,因此我们尝试滤去这部分相关性,很简单的想法是通过最小二乘法得到 \boldsymbol{y} = \boldsymbol{AX} + b 的各个参数值,另有更优的
Yule-Walker 方法:
stasmodels默认使用这一方法Durbin-Levinson 方法
这里略去 ols, yw, dl 方法的计算细节。
确定 p 值
取 p = 1, 3, 5, 10, 创建一个随机的自回归序列,对其进行 ACF 和 PACF 分析: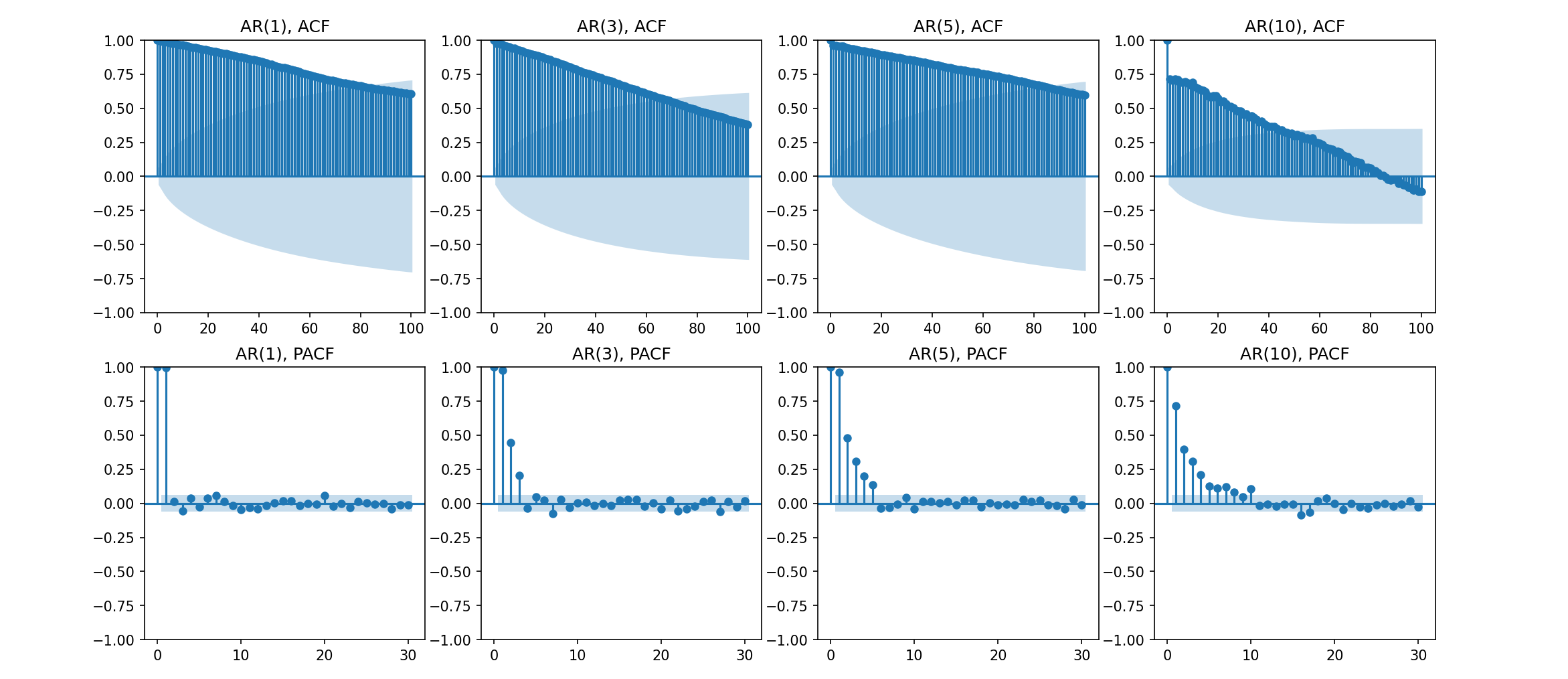
ACF 下降缓慢
PACF 通过 95% 置信区间很好地给出了 p 值
平稳性
AR 模型研究的时间序列应该是平稳的,这时常见的回归/模型才管用,因此我们引入 平稳序列 的概念
对时间序列 X_t,如果对任意 t \in \mathbb{Z} 和正整数 n, k, (X_t, ..., X_{t+n}) 总是和 (X_{t+k}, ..., X_{t+k+n}) 同分布,则称 X_t 是严平稳时间序列
现实生活中不可能验证时间序列上的两组随机变量是同分布的,所以我们引入弱化的条件:
序列 X_t是弱平稳时间序列,如果 X_t 存在有限的二阶矩且满足:
均值E(X_t)=\mu,与 t 无关
方差Var(X_t)=\gamma_0,与 t 无关
协方差\gamma_k = \text{Cov}(X_{t-k}, X_t),与 t 无关
ADF 检验
ADF 检验 (Augmented Dickey-Fuller test) 用来检验时间序列是否平稳,通过检验其是否有单位根完成。
DF (Dickey-Fuller) 检验
DF 检验仅适用于 AR(1) 模型:
构建回归模型\displaystyle \Delta y_{t}=\gamma y_{t-1}+\varepsilon_{t},其中\displaystyle \Delta y_{t} 是序列的一阶差分
确定零假设 gamma=0:存在单位根,序列不平稳
使用最小二乘法 (OLS) 确定 gamma
计算 DF 统计量\displaystyle \text{DF Statistic} = \frac{\hat{\gamma}}{\text{SE}(\hat{\gamma})}或 p-value,如果统计量小于临界值,拒绝零假设,序列平稳,反之序列不平稳
Augmented 增强
对于 AR(p) 模型,适用增强的 DF 检验
改进回归模型\displaystyle \Delta y_{t}=\gamma y_{t-1}+\sum_{i=1}^{p}\varphi_{i}\Delta y_{t-i}+\varepsilon_{t},引入了滞后差分项消除高阶自相关
其余同 DF 检验,这样,我们能够在一定显著性水平下认为序列平稳或不平稳。
序列平稳化
对于非平稳信号,要使用 AR 模型预测应当先使序列平稳化,我们要做的包括
趋势消除(计算差分)
异方差消除(求对数/RANSAC)
自相关性消除
周期性消除
并由于高次项存在的可能性,循环做上面的操作直到通过平稳性检验。
实现
ACF/PACF 序列
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
fig = plt.figure()
ax = fig.add_axes()
plot_acf(data, ax)
plot_pacf(data)
plt.show()ADF 检验
from statsmodels.tsa.stattools import adfuller
adf, pvalue, usedlag, nobs, critical_values, icbest = adfuller(x)其中,
adf: ADF 统计量
pvalue: 近似 p-value
usedlag: 使用的 lag 值(AR(p))
nobs: 观测次数
critical_values: 临界值
icbest: 根据 AIC 或 BIC 计算的最大化信息值
另可输入参数
autolag: 决定 lag 值选择方案是 AIC 或 BIC
regression: c 消除常数, ct 消除线性趋势, ctt 消除线性和二次趋势, nc 不消除
附录
ACF/PACF 绘图
import numpy as np
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
def ar(p, n, phi):
x = np.zeros(n)
for i in range(p):
x[i] = np.random.normal(loc=10, scale=1)
for i in range(p, n):
for j in range(p):
x[i] += phi * x[i-j-1]
x[i] /= p * phi
x[i] += np.random.normal(loc=0, scale=2)
return x
p = [0, 1, 3, 5, 10]
for i in range(1, 5):
data = ar(p[i], 1000, 0.8)
plt.subplot(2, 4, i)
ax = plt.gca()
plot_acf(data, ax, 100)
plt.title(f'AR({p[i]}), ACF')
plt.subplot(2, 4, i + 4)
ax = plt.gca()
plot_pacf(data, ax)
plt.title(f'AR({p[i]}), PACF')
plt.show()