这是 2025 春 计算机视觉导论的笔记
Todo:
- 内容杂乱无章,十分愚蠢,或许未来会润色语言使它便于阅读
Review
- 目标:Lane Detection
- 完成的部分:Edge Detection
- 现在的目标:从散点到直线,得到更好的 Line Fitting
Least Square Method
- Least Square Method:L2 norm - Find (m, b) to minimize \displaystyle E = \sum_{i=1}^n (y_i - mx_i -b)^2
-
let \displaystyle Y = \left[\begin{matrix}y_{1} \\ \vdots \\ y_{n} \end{matrix}\right] , \displaystyle X = \left[\begin{matrix}x_{1} & 1 \\ \vdots & \vdots \\ x_{n} & 1 \end{matrix}\right], B = \left[\begin{matrix}m\\b\end{matrix}\right], \displaystyle E = ||Y-XB||^2, finally gives \displaystyle B = (X^TX)^{-1}X^TY,必要数学参见 matrix cookbook
-
一个凸优化问题,且具有唯一全局最小值
-
Limitation: For outlier, it's not robust, 离群点会把线全部带偏; fails for vertical line
-
Improvement: Use \displaystyle ax+by=d, to maxmize E, data \displaystyle A = \begin{bmatrix}x_{1} & y_{1} & 1 \\ \vdots & \vdots & \vdots \\ x_{n} & y_{n} & 1\end{bmatrix}, \displaystyle \boldsymbol{h} = \begin{bmatrix}a \\ b \\ d\end{bmatrix}. 此时得到的最小二乘回归方程 \displaystyle \boldsymbol{Ah} = 0,并满足 \displaystyle E=||\boldsymbol{Ah}||^2 最小;它有一个平凡解 (0, 0, 0);指定 \displaystyle a^{2}+b^{2}+d^{2}=1 可以让解唯一化,失去平凡解
-
- Solve:Find \displaystyle \boldsymbol{h}, minimize \displaystyle ||\boldsymbol{Ah}||, subject to \displaystyle ||\boldsymbol{h}||=1
- 问题转化:找到单位球面上的一个点使得这个点和A的点积最小
- 方阵矩阵的特征值分解:实对称方阵一定可以对角化 => 解 \displaystyle Bx=\lambda x 得到 n 个特征值 \displaystyle \lambda 和 \displaystyle x_{i} => 凡是可以对角化的矩阵 n 个特征向量构成正交基 => 取最小的 \displaystyle \lambda 时 \displaystyle ||\boldsymbol{Bh}|| 最小 (把对应的维度压缩到最小)
- 非方阵矩阵不能做特征值分解/对角化 => 提出了一种从方阵到非方阵的extension:Singular Value Decomposition (SVD)
- Analysis:Robustness Absolutely still sensitive to outliers; 这来自 L2 Norm 越离群 gradient 就越大的特性; 如果用 L1 Norm?收敛就很困难
RANSAC
Random Sample Consensus: 解决离群点的问题
- 自动丢掉离群点的方法:如果已经知道了答案,离群点就会离它significantly地远;那么就随机取出一个Sample,求这个Sample构成的hyperplane(如果Sample数大于维度就要最小二乘或SVD了,等于维度就可以直接求解线性方程组),再衡量Consensus,让支持它的dataset里尽可能没有outlier
- RANSAC Loop
- Initialize: 随机取 2 个点 (期望不包含Outlier,所以是最少的可以形成hyperplane的seed group)
- Compute: transformation from seed group
- Inliers: 计数合群点的数目,更新最大Inliers => 找到Inliners最多的那个Sample
We should implement a parallel version: Use Tensor, No For Loop
- Hyperparameters
- Hypothesis: 取出多少个点做Sample
- Theoshold: 算作Inlier的阈值 (例如 \displaystyle 3\sigma)
- Post-process:如果多个seed group给出了相同的Inlier number?朴素的优化 => 把这些Inlier选出来,用最小二乘或SVD给出最后的结果的那个方程
- 为什么要选最小数目的hypothesis?包含n个点的hypothesis全都正确的概率是 \displaystyle \omega^{n},所有的k个sample全部fail的概率是 \displaystyle (1-\omega^{n})^{k},所以需要尽量减小n,增大k
- Pros and Cons
- Pros: general, easy
- Cons: only moderate percentage of outliers => Voting Strategy, Hough Transform
Summary
gradient -> edge -> line
这个是 module-based system,缺点是一步出错就会影响很多,需要很强的robustness;自动驾驶从几十万行的rule到End2End的system也是这样的;
Lecturer: 某司唯一的不端到端的是提取出红绿灯🚥结果识别,再丢进网络里;
这部分总之只是对经典视觉方法的管中窥豹;
Corner Detection
- 图片的 keypoints 也是很重要的东西,应用例:从关键点检测keypoints localization,到corri-bonding到image matching到相机的rotation/transform的识别
- Requirements
- Saliency: Interesting points
- Repeatability: same result, same object, different images
- 对亮度的不变性 Illumination invariance
- Image scale invariance
- Viewpoint invariance
- implant rotation: 关于相机主轴的旋转
- affine: 产生仿射变换 (?)
- Accurate localization
- Quantity: number sufficient
- Corner
- 基本满足上面的requirements
- key property: in the region around the corner, image gradient has two or more dominant directions
- Harris Corner: Use a Sliding Window
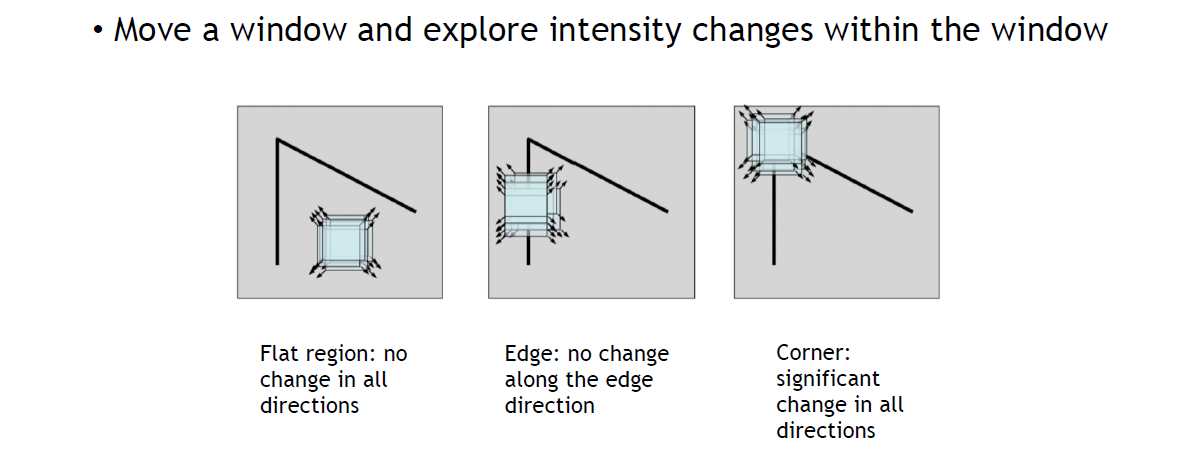
留意我们没有再进行edge detection,这里衡量gradient的方法是滑动窗口内的intensity
- Implement
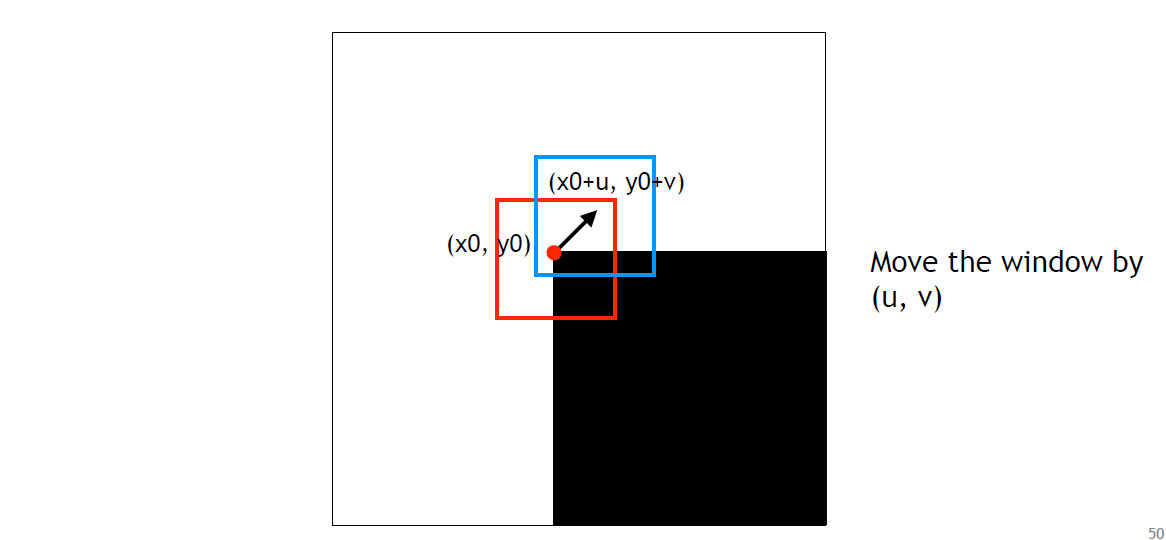
- Move
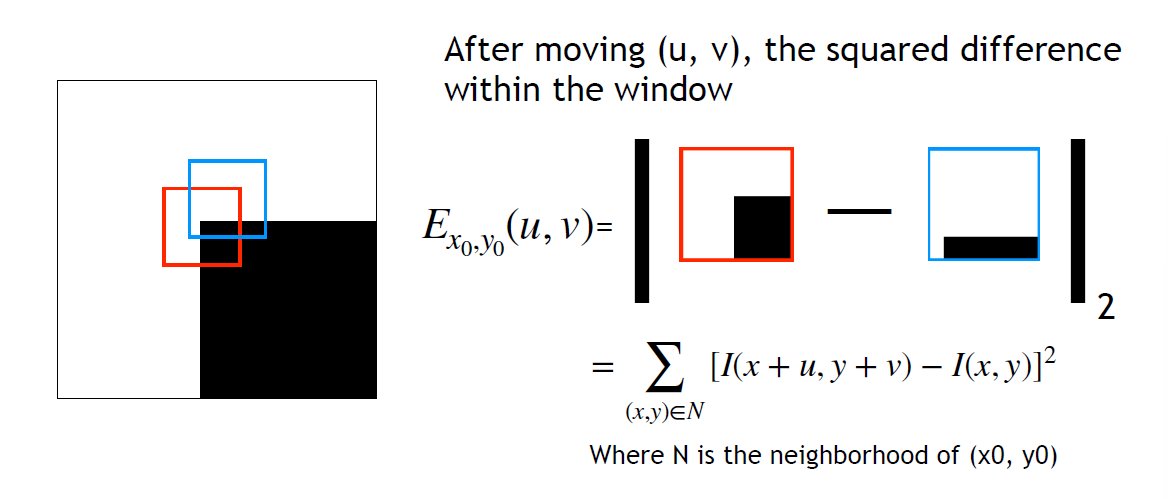
- Square diff
- Window function

- Let Square intensity difference \displaystyle D(x, y)=[I(x+u, y+v)-I(x, y)]^{2}
Window Function \displaystyle w(x,y) which has a param \displaystyle b
=> 成为一个卷积操作\begin{align}\displaystyle E_{x_{0},y_{0}}(u,v) & =\sum_{x,y}w^{\prime}_{x_{0},y_{0}}(x,y)[I(x+u, y+v)-I(x, y)]^{2} \\ & =\sum_{x,y}w(x_{0}-x,y_{0}-y)D_{u,v}(x,y) \\ & =w*D_{u,v}\end{align}- 在 \displaystyle (x_{0},y_{0}) 周围关于 \displaystyle (u,v) 做一阶 Taylor 展开,进而把 \displaystyle D 写成二次型
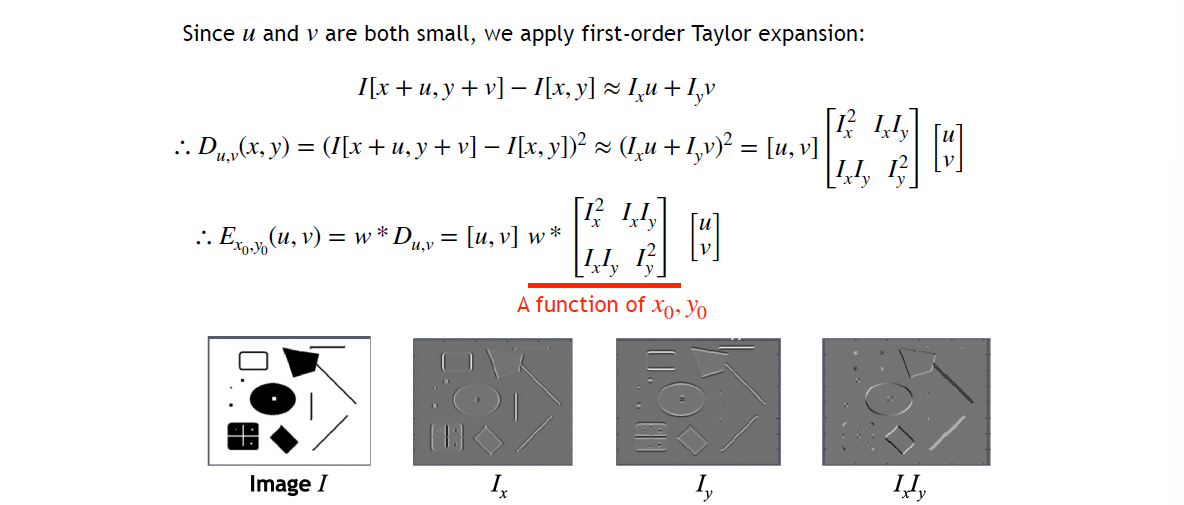
注意每个I都是一个大的image - Result
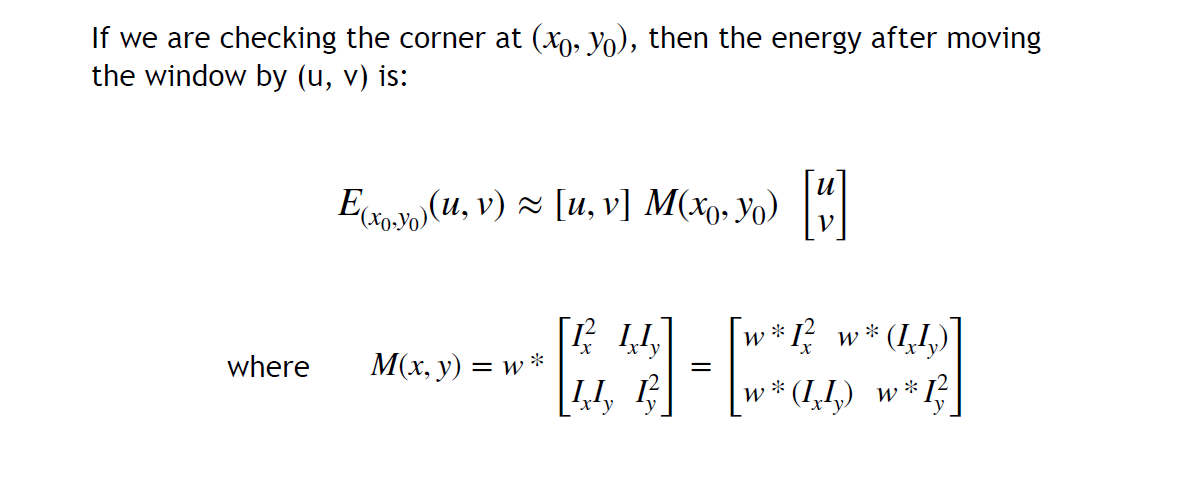
- Analysis


- Corner/Edge/Flat?
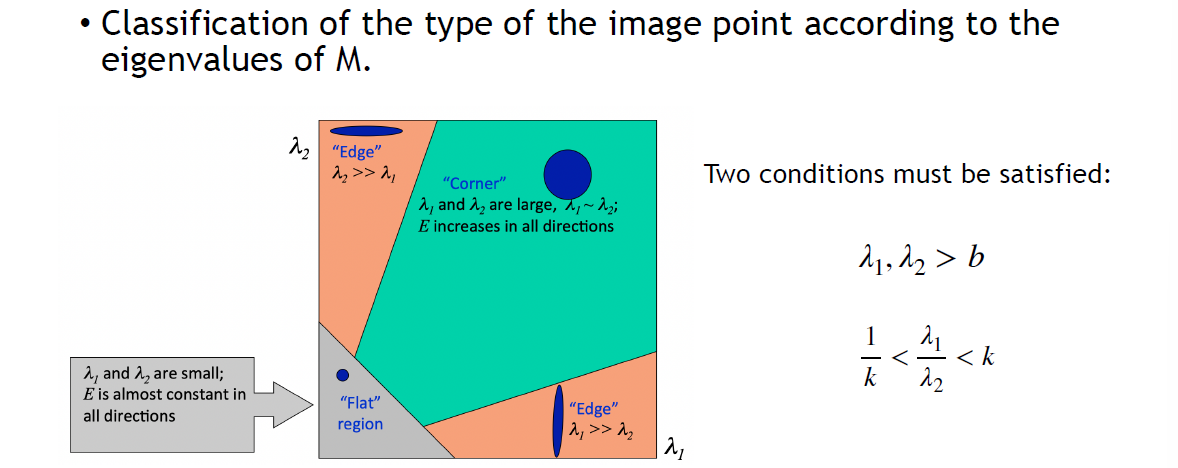
- 问题:多大算大?可能需要多个超参,但我们只关心corner,可以定义

- let window rotation-invariant => Gaussian window
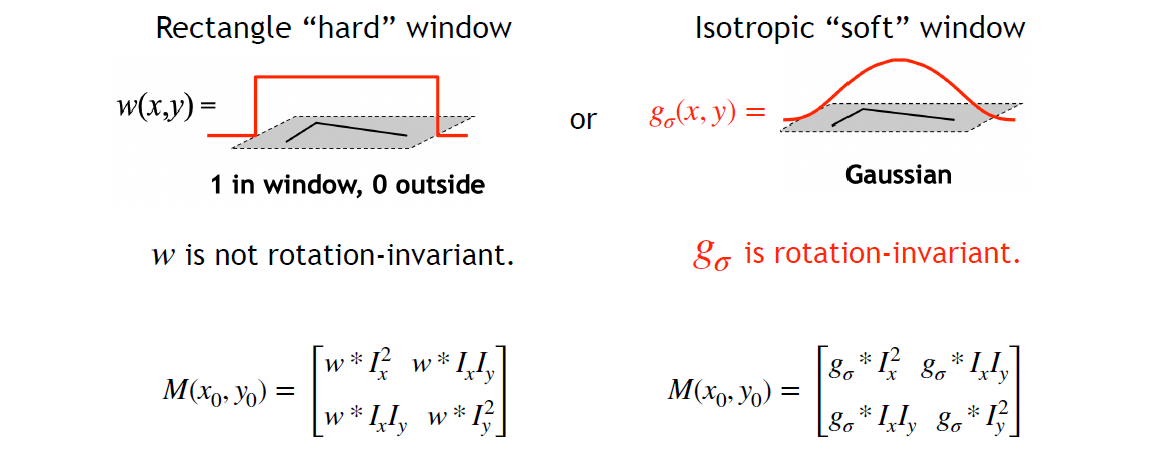
- 在 \displaystyle (x_{0},y_{0}) 周围关于 \displaystyle (u,v) 做一阶 Taylor 展开,进而把 \displaystyle D 写成二次型
- Move
- Whole Process

这一部分推导
Properties
Definitions
If \displaystyle X\in V, and \displaystyle f:V\to V is a function, \displaystyle T:V\to V is a transformation operation like translation or rotation, then
- \displaystyle f to be equivariant under \displaystyle T if \displaystyle T(f(x))=f(T(x))
- \displaystyle f to be invariant under \displaystyle T if \displaystyle f(x) = f(T(x))
- Scale
- Harris Detection 对 translation 和 rotation (?) 都是 equivariant 都是等变的
- To be realistic, 旋转后对网格进行了双线性差值,自然都不可能是rotation-variant的
- 对 scale 不是 invariant 的 (自然也没有equivariance),但问题不大
- Scale-invariant methods: Harris Laplacian 和 LIFT