Depth Image

Review

上节我们已经讲了Depth Image+\displaystyle K,R,T才是真3D，单独的 z depth 不能表示世界坐标系里的距离信息——当你指出图中的这个点 \displaystyle (u,v) 的 z depth 或者 ray depth 是 \displaystyle d，你无法知道它对应真实世界的哪个点，势必要知道相机的intrinsics先back

Sensors

我们简单熟悉Depth Sensors，它们具备（裁切空间）FoV，near plane，far plane参数；其中实验室里经常用到的有 Stereo Sensors（双目相机），如下图左；基于双目改进的 Structural light（结构光）方案如下图右，它有一个 RGB Camera，一个IR Projector（红外投影），两个IR Receiver

Stereo Sensors

最baseline的双目相机得到深度的过程：

1. 找到左右眼两个相纸上相同的点
2. 进行 \displaystyle y 高度对齐，这时左右眼同一点的位置分别是 \displaystyle u, u^\prime
3. \displaystyle u-u^{\prime} 就是视差 disparity
4. 用相似就能算出来 z depth

当然还有一个问题是如何找到左右眼的相同点（Correspondence）？可以用一些传统的feature descriptor来匹配相同点（当然也能用神经网络匹配），我们也学过了harris corner detection；

另外，我们也关注到左右眼会存在盲区（只有一只眼睛能看到的图像部分），这样的部分就是missing disparity，我们算不了它的depth

Cons: 很多correspondence的确定是困难又不准确的，想象一块没有纹理的白板，你如何确定哪个点和哪个点对应？就是人眼处理这个task也很难；想象一块镜面/玻璃，面上的同一点左右眼看到的干脆不是同一点了（镜面反射or折射），综上我们觉得

• Stereo方案适用于漫反射表面（diffuse surface/lambertian surface）
• 对白板/镜面/透明，仅仅靠两幅可见光的RGB确定深度根本是不可能的了

Structural Light

那我们自然的想法就是人为地project一些特征（画在无纹理的表面上），就可以解决没有Texture的表面无法定位的问题，这个叫 Active Stereo；

用红外光投射一个便于定位/correspondence的光斑图的方案就是 Structural Light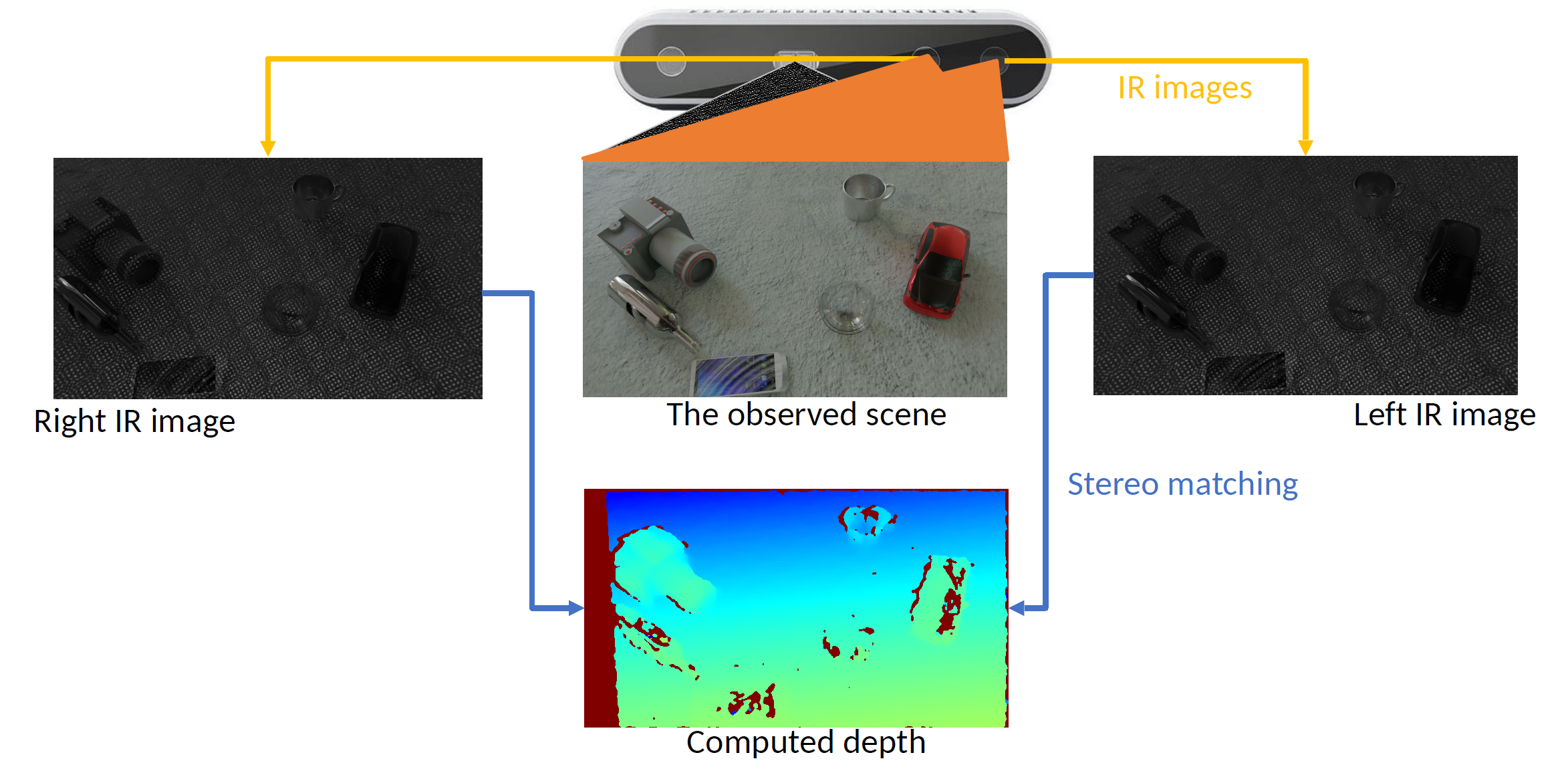

Cons 它也解决不了镜面/透明的问题；另外，很重要的问题是倘若场景里存在更强的 IR Source（比如太阳！），IR Image会被很大地干扰；如果 IR 打在特别黑的吸光材料上，也会失效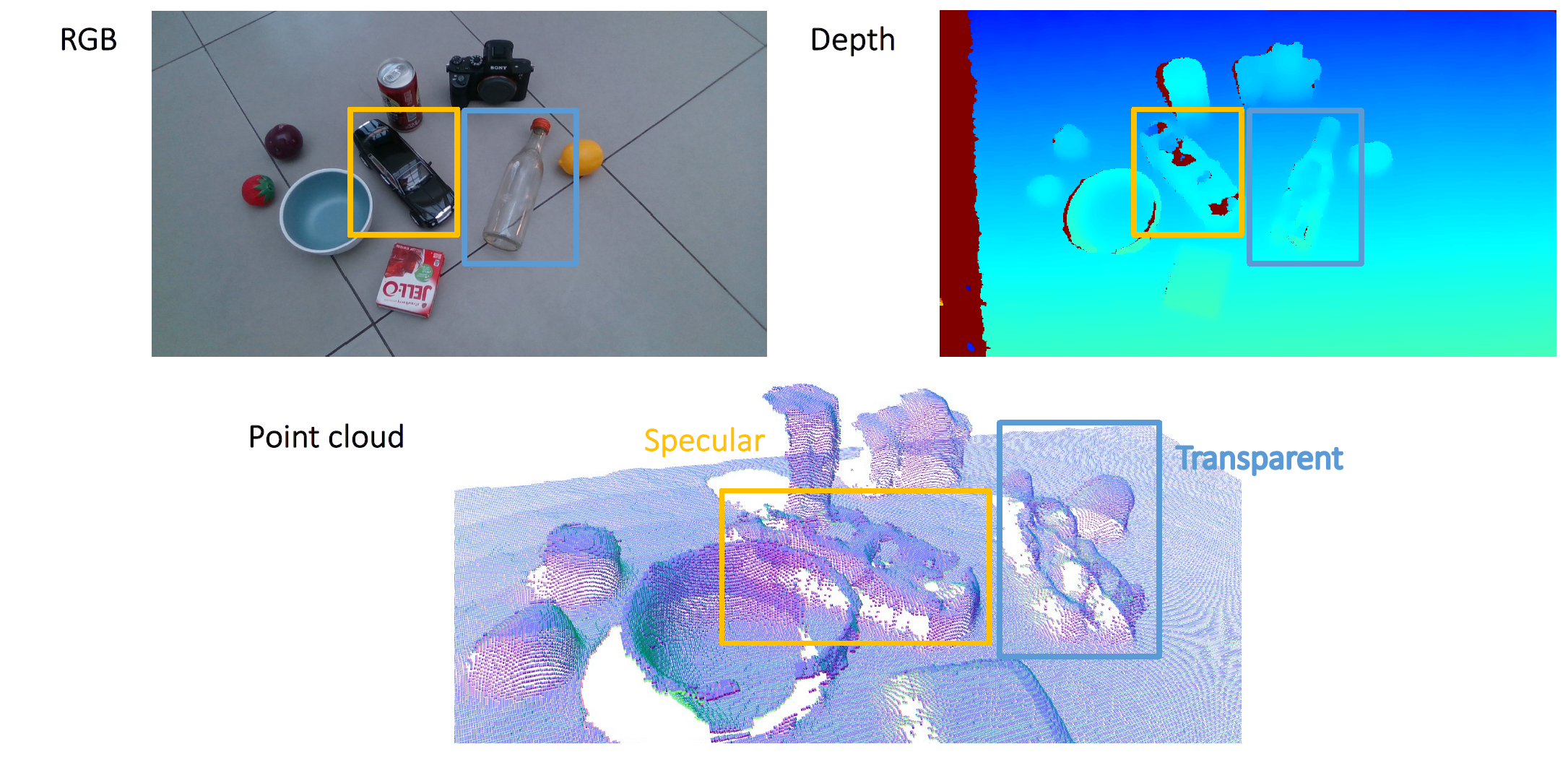

Quiz: 为什么激光雷达得到的是 ray depth，stereo 得到的天生就是 z depth？激光雷达能不能解决镜面/透明问题？

Voxels

Pros

1. \displaystyle H\times W\times D 很规整，很好indexed

Cons

1. \displaystyle O(n^3) 比 \displaystyle O(n^2) 简直是飞跃，resolution 负担很重，占用很大

Mesh

这个我们可太熟悉了，这部分记录一些零散的知识

1. 用三角面/四边面构成几何体的表面，有精度/Resolution/LoD
2. 三角面在镶嵌问题上是最优的，四边面用起来是因为建模的时候规整便利
3. Mesh 可以看成一个图 \displaystyle \{vertex, edge\}，可以表示为
   1. \displaystyle V=\{v_{1},v_{2},\dots,v_{n}\}\in \mathbb{R}^3
   2. \displaystyle E=\{e_{1},e_{2},\dots,e_{k}\}\in V\times V，是\displaystyle V和\displaystyle V的一个直积
   3. \displaystyle F=\{f_{1},f_{2},\dots,f_{m}\}\in V\times V\times V
4. 像 PBR, 路径追踪, render pipeline 我们当然也能作为mesh的feature去研究，我们今天就不关心了
5. 存储格式：OBJ
   有趣的是这里每个triangle的顶点顺序不是随便的，按照右手定则确定面的朝向/法向量
6. Geodesic Distance: the shortest distance from one point to the other point on the surface, mesh 上的最短路确定（还挺麻烦的），存在例如 Fast Marching Method 的方法

Point Cloud

1. \displaystyle \mathbb{N}^3， 无序的，比起说是一个vector更准确地说是一个set
2. Pros 存储友好，易于看懂；Cons 没有surface信息
3. “surface是一个二维流形，point cloud 是在surface上的一个采样sampling”

Sampling Strategy: Uniform Sampling

先定义任务：我们希望把Mesh转换成point cloud，为此需要一个保证uniform的采样策略；具体地，这样的策略应该满足

1. triangle面积作为选中这个triangle的probability weight
2. 在triangle内部，采样的分布应该满足对任意的子面积 \displaystyle S^\prime, 采样点的个数 \displaystyle n 满足 \displaystyle \frac{n}{N}=\frac{S^\prime}{S}

Step 1 很简单，Step 2 我们要想一想：一个可行的策略是把三角面镜像成平行四边形，在长和宽上独立地uniform随机 \displaystyle (a_{1},a_{2})，对应的点 \displaystyle v_{1}a_{1}+v_{2}a_{2} 如果在镜像三角形里，镜像回去就行

Cons 只是数学期望上uniform，真的均匀并不是很确定的事情，会有的地方因为lucky就是更加密
更想要的结果：

Sampling Strategy: Iterative Furthest Point Sampling

我们重新更好地定义任务（Farthest Point Sampling, FPS）：找到一个分布使得 \displaystyle \frac{n(n-1)}{2} 对点两两之间距离的和最大，可惜这被证明是 NP-Hard 问题，难以在多项式时间内解决；一个 greedy approximation method 是 Iterative FPS，第 1 步取一个比目标密度更dense的值n oversample，作为待选；第 2 步先随便找一个点，再找离它最远的点2，再找离这俩最远的点3，...，点k；这个方法大致是 \displaystyle O(nk) 的。

这貌似是老师自己的成果

Distance Metrics

Irregular data 的 distance 是很 tricky 的事情，需要根据具体任务而定；有两个例子：

1. Chamfer distance (\displaystyle O(n^2)) define \displaystyle d_{CD}(S_{1}, S_{2})=\sum_{x\in S_{1}}\min_{y\in S_{2}}||x-y||_{2}+\sum_{y\in S_{2}}\min_{x\in S_{1}}||x-y||_{2}
2. Earth Mover's distance (hard) define \displaystyle d_{EMD}(S_{1},S_{2})=\min_{\phi:S_{1}\to S_{2}}\sum_{x\in S_{1}}||x-\phi(x)||_{2}, where \displaystyle \phi:S_{1}\to S_{2} is a bijection.

Chamfer 只在意谁和它最近，不存在供求关系所以对sampling是insensitive的；EMD 需要一一配对，如果一个地方供不应求就可能到很远的地方去寻找朋友，所以对sampling是highly sensitive的。

3D Deep Learning

Problem: define CNN for Point Cloud?

我要先胡思乱想一会：首先输入是一堆无序的 \displaystyle (x,y,z)，如果说conv是高斯模糊是weight可训练的加权平均，那这里的Conv就应该是 \displaystyle \sum_{i} w_{i}(x_{i}, y_{i}, z_{i})，可以想象它会让一组点在空间聚类(？)映射到另一个点，信息浓缩的任务应该可以完成；问题是 \displaystyle i 指标怎么取？一定不能是1d-CNN那样连续的取i，因为是无序的；如果遵循我们是对空间距离近的一组点同一的处理，那么应该先做一个预排序使得一个连续的\displaystyle i区间对应的点总在一坨？似乎没有什么毛病，这样我们的input_size就是 \displaystyle (C\times 3\times N)，相当于一个2d-CNN处理 \displaystyle (3\times n) 的窗口。但是很有问题啊！这个预排序怎么做到呢？2d img只有2个移动方向，要么u，要么v，所以我们遍历了所有的(u, v)，但是这里不对！我的预排序会让一个点只出现「窗口大小\displaystyle n」次，我很怀疑能不能捕捉到合适的特征。如果以表面为工作平面，我希望能达到这样的效果？
这样是不是要先根据表面展开point cloud？这会非常复杂...如果以体为单位？
这样似乎每个固定大小体内部点的个数会不同。

\displaystyle 3\times N+MLP的问题：例如先排\displaystyle x，再排\displaystyle y，再排\displaystyle z，随便换两个点feature就全不行了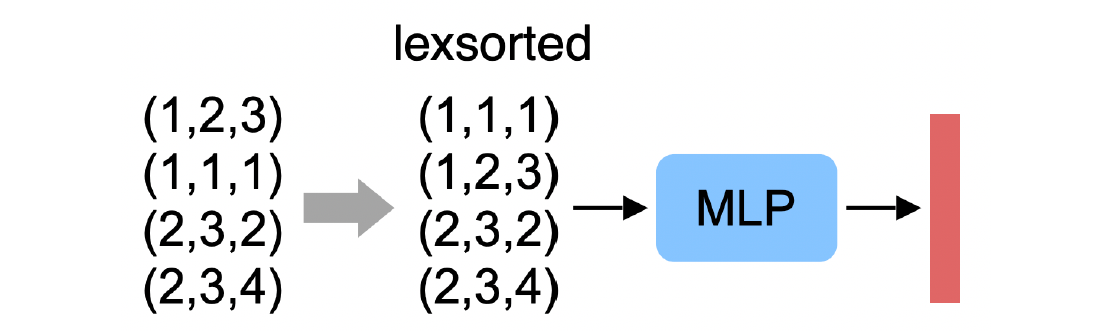

PointNet (Qi et al. 2017, CVPR)

1. Symmetric Function: 我们希望使用Permutation invariant的函数（例如sum avg和max）构建一个神经网络；
2. 核心想法：
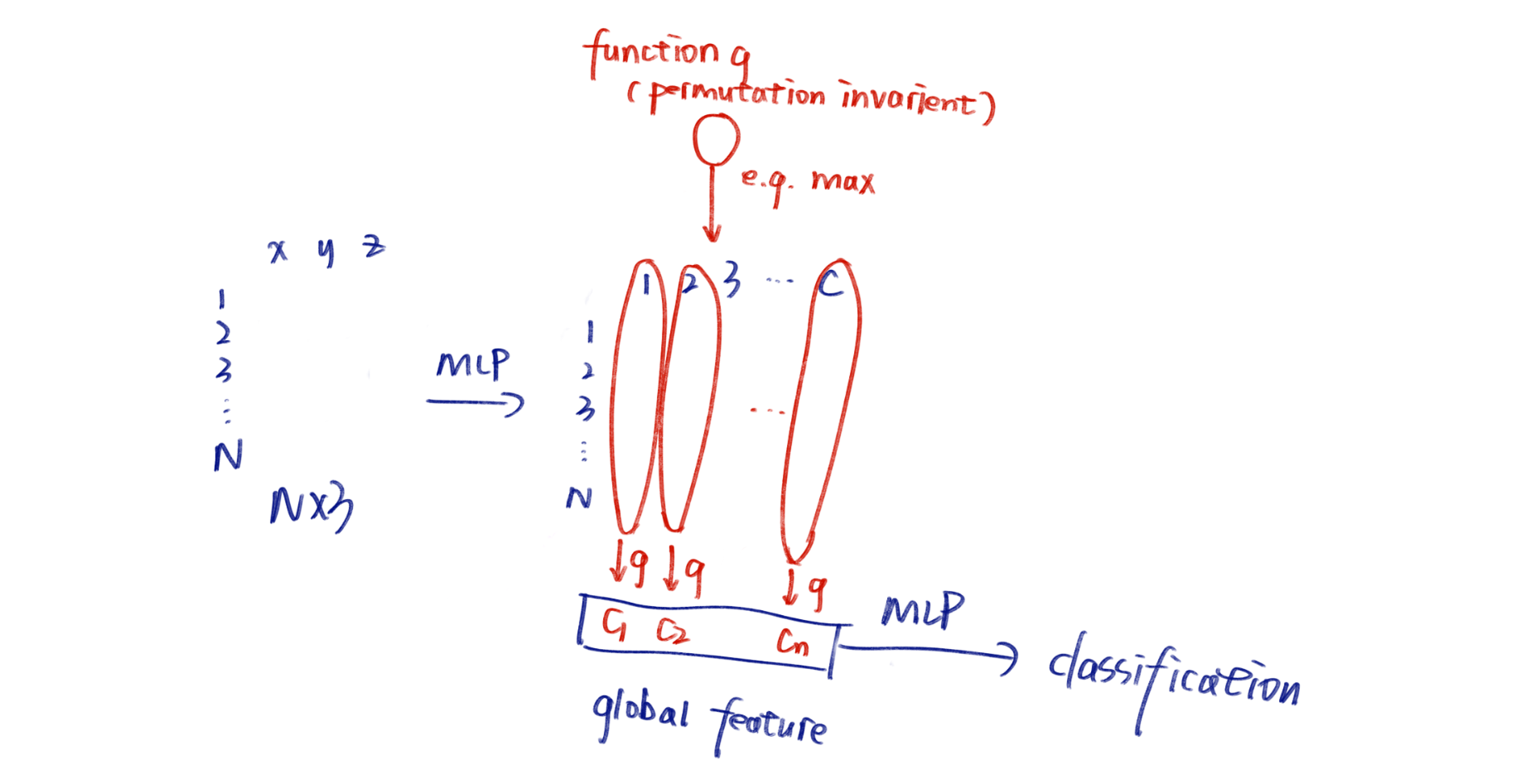
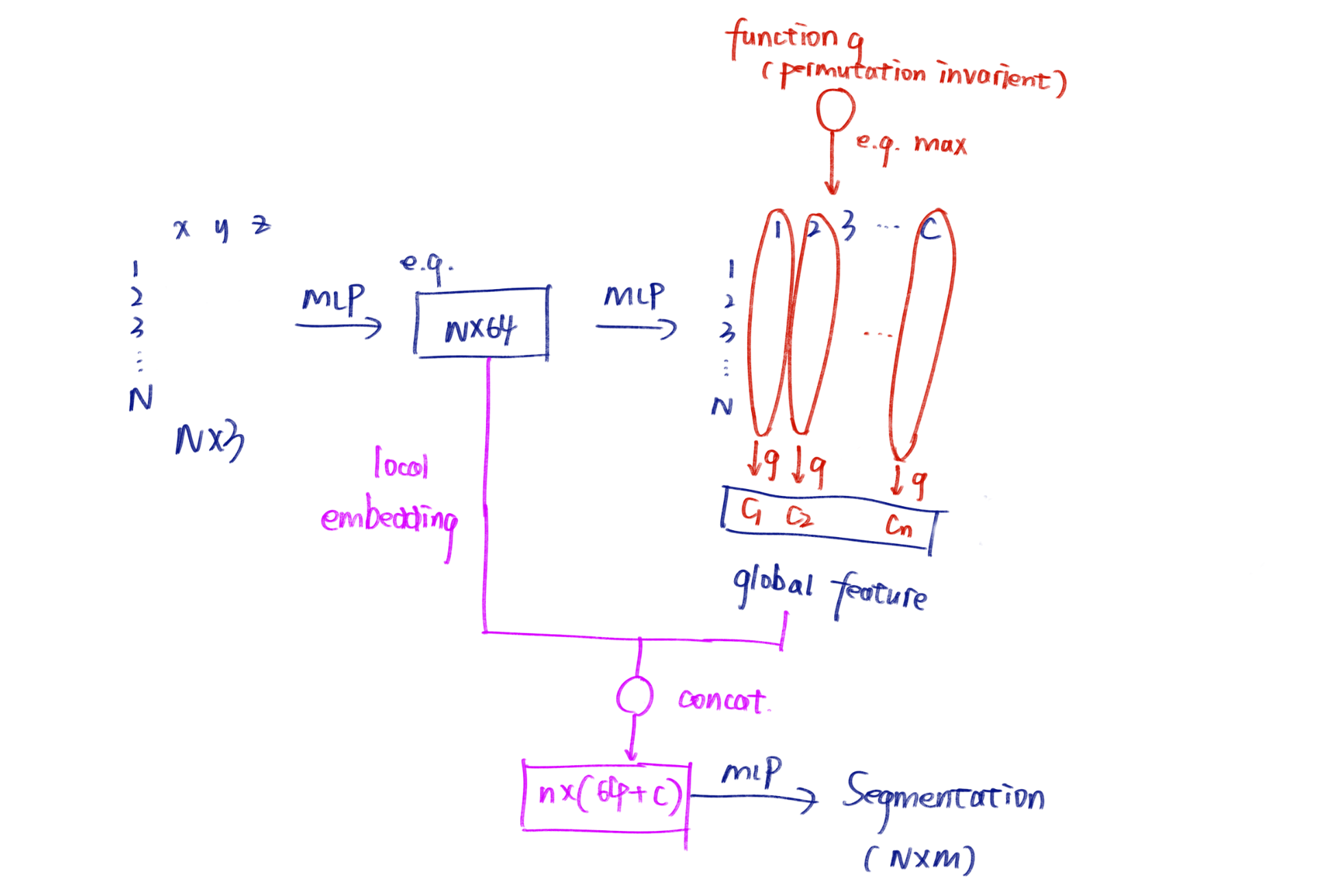
3. 其中的transform后来证明是没有用的

神奇的性能：

1. params -80%
2. FLOPs -88%
3. robustness to resolution (less than 2% acc drop with 50% missing data!)

为什么如此robusted？因为它在function g那里丢掉了特别多的冗余信息，可视化说明它自己学会了提取critical point；它对点的总数n也特别robust(这是因为那个很巧妙的C维特征方法完全地permutation invarient)

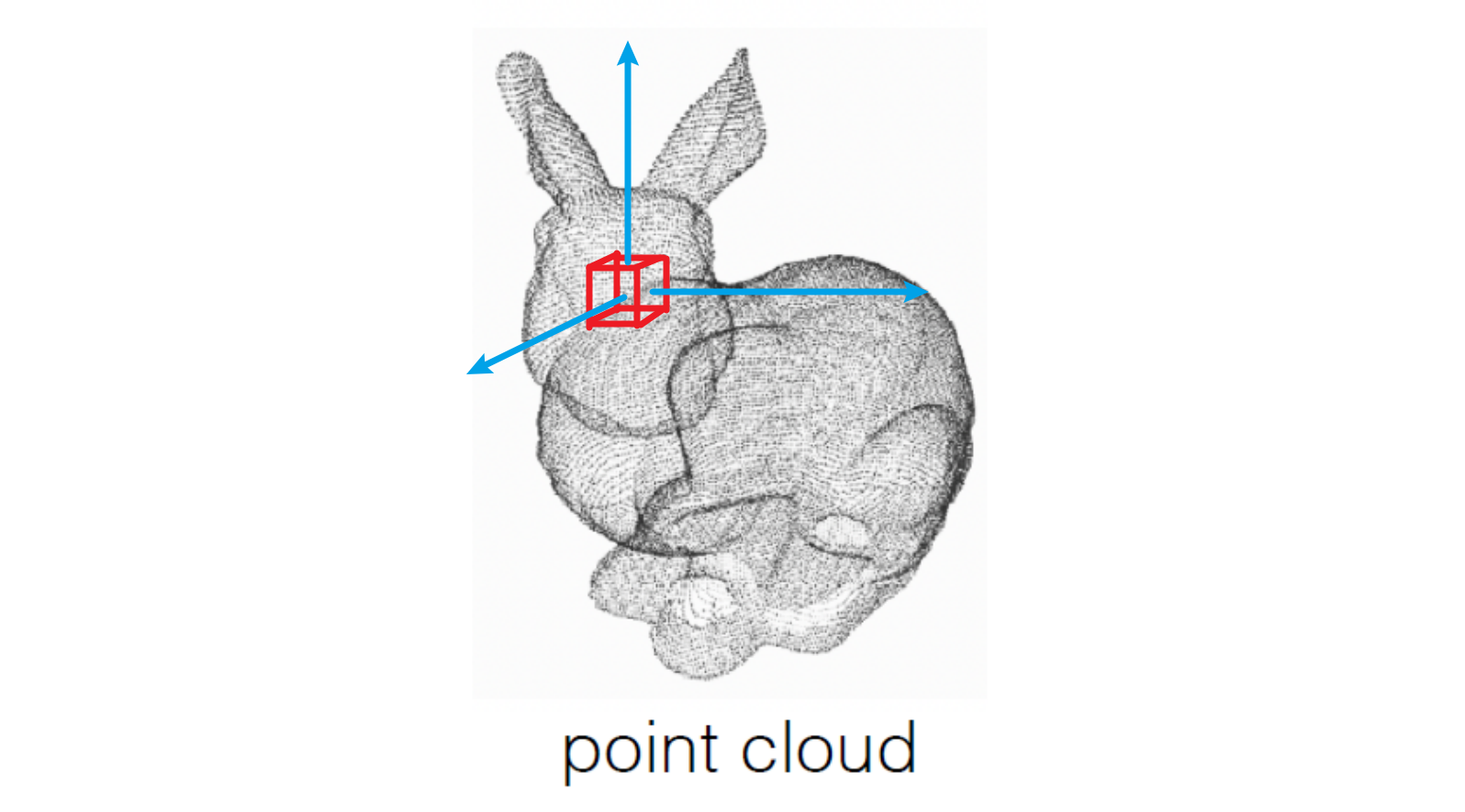
Cons 它和周边的信息不会交互所以不会提取局部特征，较3D CNN没有很好的涨点；所有点云center都对齐到原点，如果所有点向上提高1格，那么所有的feature都变了，结果是很差的；

PointNet++ (Qi et al., NIPS 17)

聚焦局部特征的提取 Tl;DR:

1. 层级化feature extraction
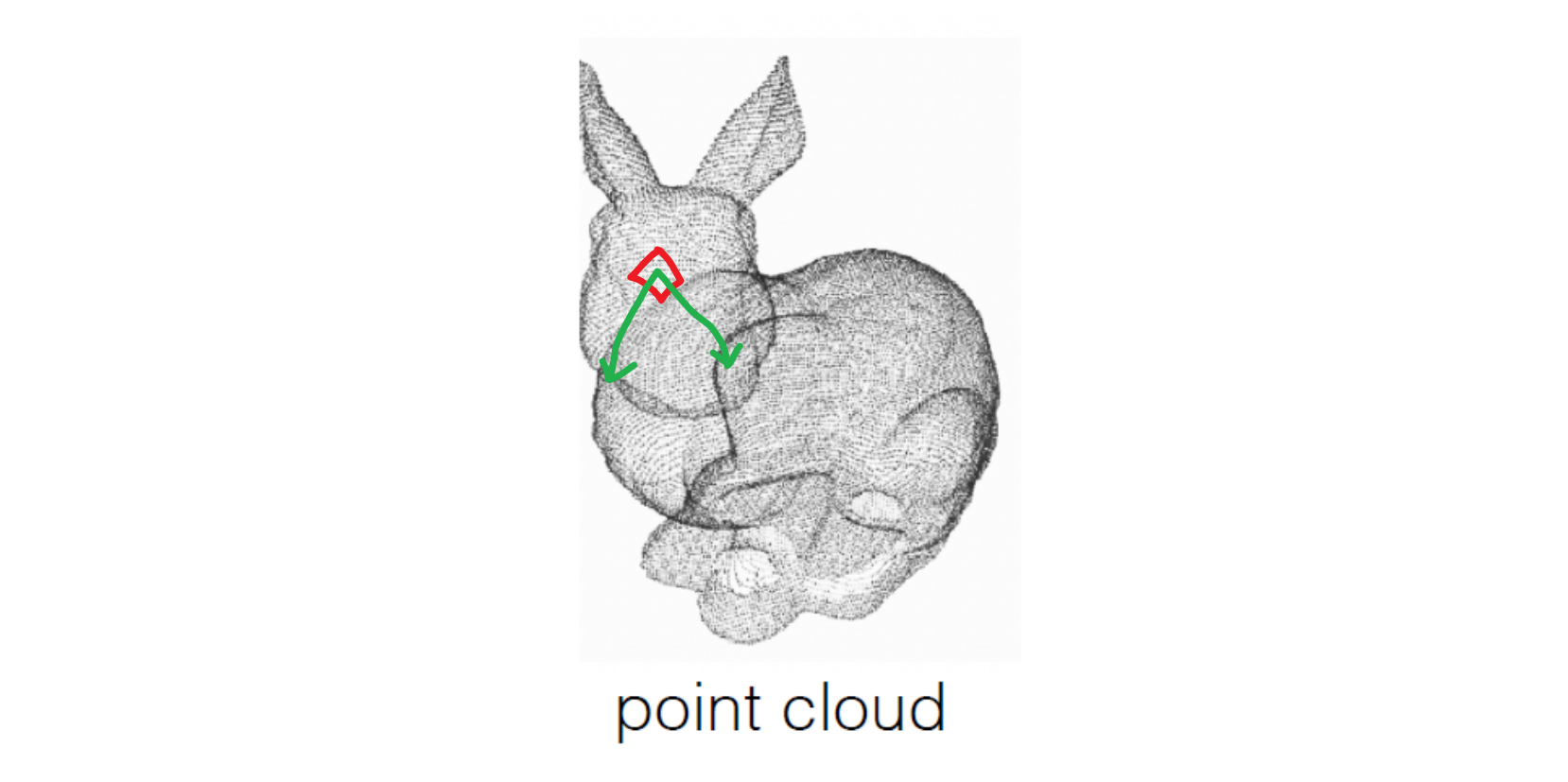
2. relative, no absolute coordinates

Ball query

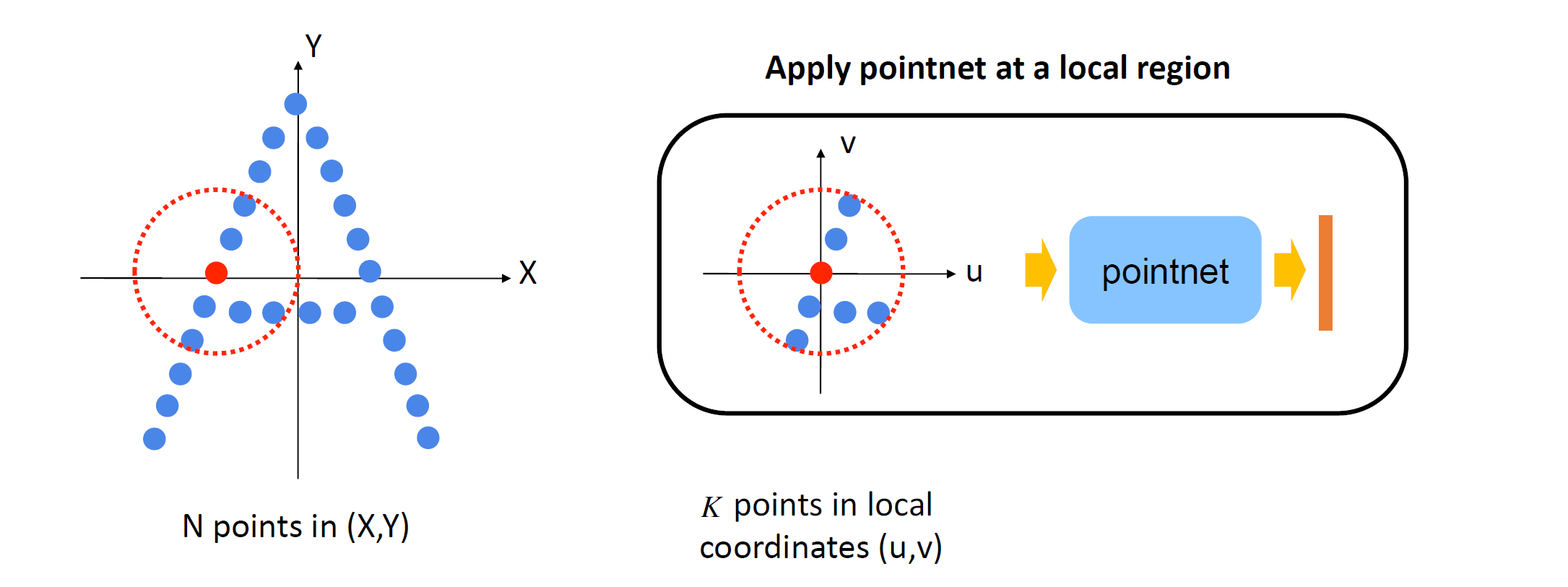
1. Ball size: hyperparameter; set max number of points in a ball k
2. points > k => random get k
3. points < k => copy ans paste some
4. K个点的relative coord \displaystyle (u,v) 塞进 PointNet 里得到 local feature \displaystyle f，合并ball center的坐标得到特征点 \displaystyle (x_{0}, y_{0}, f)
   这称为一次 Set Abstraction: FPS+grouping+pointnet

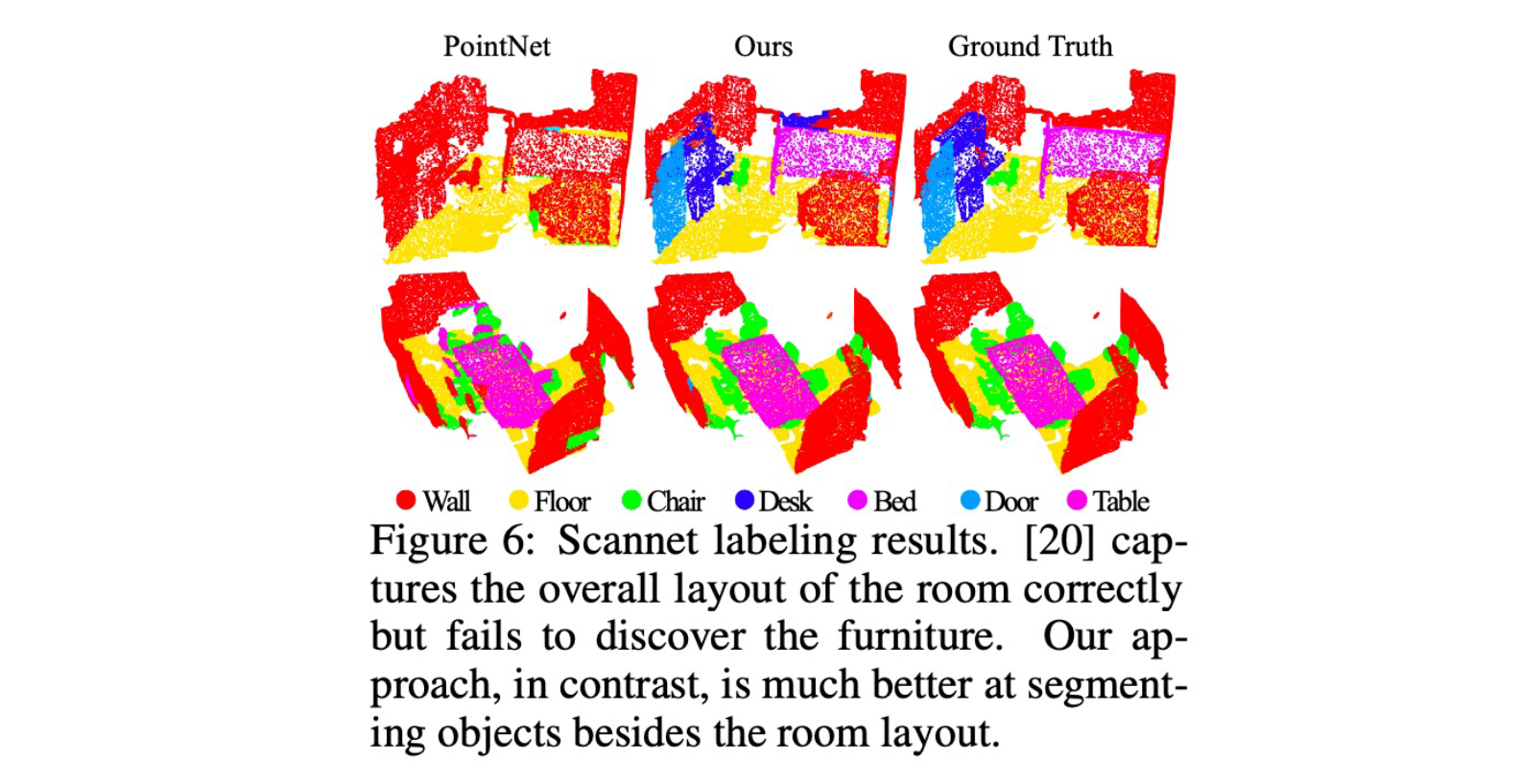
Classification

Segmentation

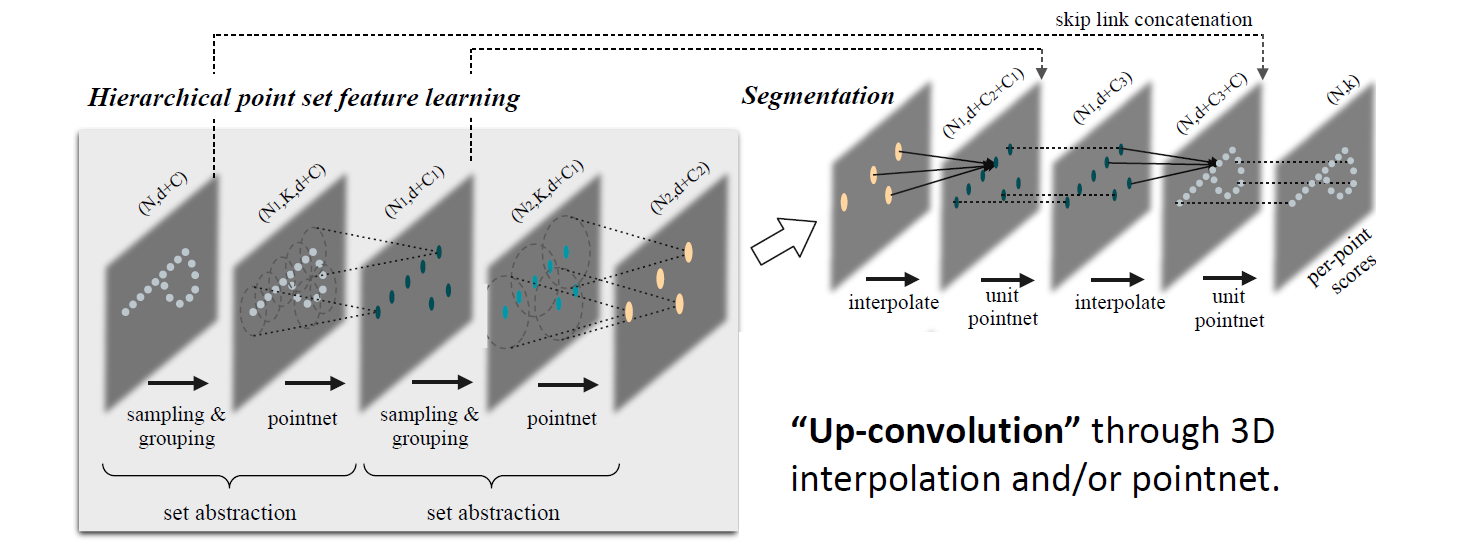
特别好的Segmentation结果