这是 2025 春 计算机视觉导论的笔记

Todo:

• 内容杂乱无章，十分愚蠢，或许未来会润色语言使它便于阅读

Feature Description

1. 我们现在在做什么：non-learning based method \displaystyle \to learning based method
2. 传统方法设计的 Feature Descriptor 面对广泛的世界环境变得不可用，把对局部的描述交给 Learning
3. Feature: any piece of information which is relevant for solving the computational task related to a certain application
   1. drop non-useful features
4. Model
   1. Heuristic model: 拍脑袋
   2. Parametric model: 参数完全由数据拟合
5. non-learning 到 learning 是 光滑的 过渡

Machine Learning 101

经典的例子：数字分类 MNIST

1. Task
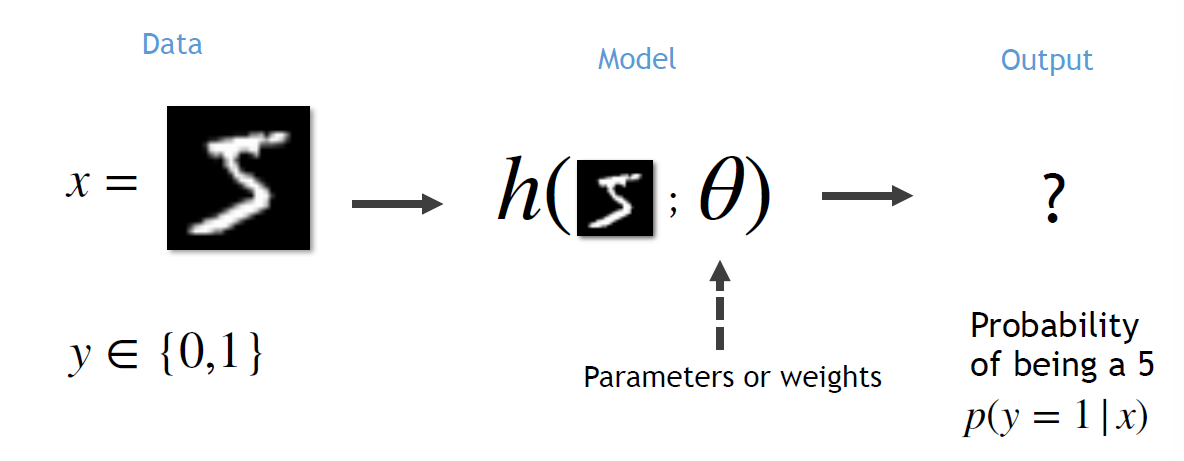
   1. Output 为什么是 Probability: 更多的优化手段
2. Prepare the data
   1. From MNIST: 70000 imgs, 28 \displaystyle \times 28, 今天的问题简化到「是否是5」
3. Built the model
   1. 粗暴的 Logistic Regression: flatten to 1-D vector \displaystyle \mathbb{R}^{784}
   2. let \displaystyle \theta \in \mathbb{R}^{784}, function \displaystyle g = \theta^{T}\boldsymbol{x}
   3. then, use sigmoid \displaystyle \frac{1}{1+e^{ -z }} 把 \displaystyle g 的结果映射到 \displaystyle [0, 1]
   4. 问题: 函数 \displaystyle g 中包含能完美分类的函数吗？先假设存在？
4. Decide the fitting
   1. let loss = square? 这是没有根据的
   2. 沿着概率论的方向前进
      1. 最大似然估计 maximum likelihood estimation MLE:
         \displaystyle \boldsymbol{P} = \prod P(x_{i}, y_{i}) = \prod\left\{\begin{align} & p,&y_{i} = 1 \\ & 1-p, & y_{i}=-1\end{align}\right.
      2. Maximum \displaystyle \boldsymbol{P} (命中可能性的乘积 => 全部命中的概率)
      3. 求 likelihood 的最大值
   3. 藏起来分类讨论
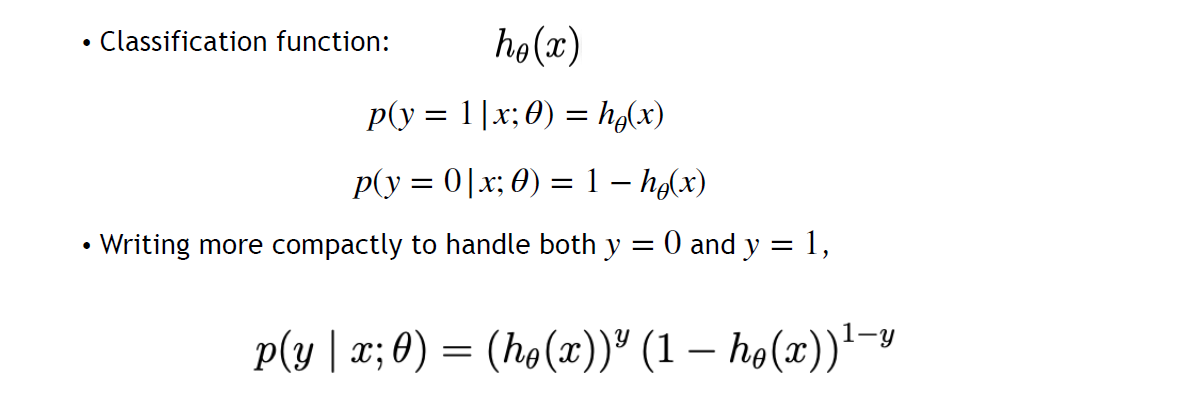
   4. 乘积 => 数学取巧之求对数
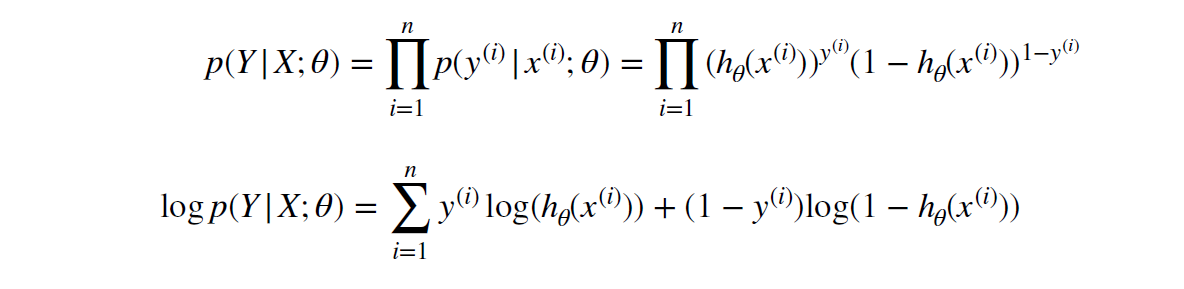
   5. 有趣的历史遗留：永远做 Minimize
      NLL Negetive Likelihood Loss: Loss = \displaystyle \mathcal{L}(\theta) = -\log p(Y|X;\theta), Minimize Loss
5. Optimization 101
   1. Loss 是没有解析解的
   2. 或许 Loss 是凸的？
      如果 NLL 是凸的，那么可以简易地解析地给出最低点，可惜 NLL 是坑坑洼洼的
   3. gradient descent (GD)：一阶的optimization方法，显然只会收敛到局部最小
      1. Update rule: \displaystyle \theta := \theta - \alpha \nabla_{\theta}\mathcal{L}(\theta)
      2. 超参 \displaystyle \alpha: 太小就太慢，太大就 overshoot
      3. 接受这个现实！
   4. GD Implement
      1. For Sigmoid, \displaystyle g^{\prime}(z)=g(z)(1-g(z))
      2. 对 Loss 求导
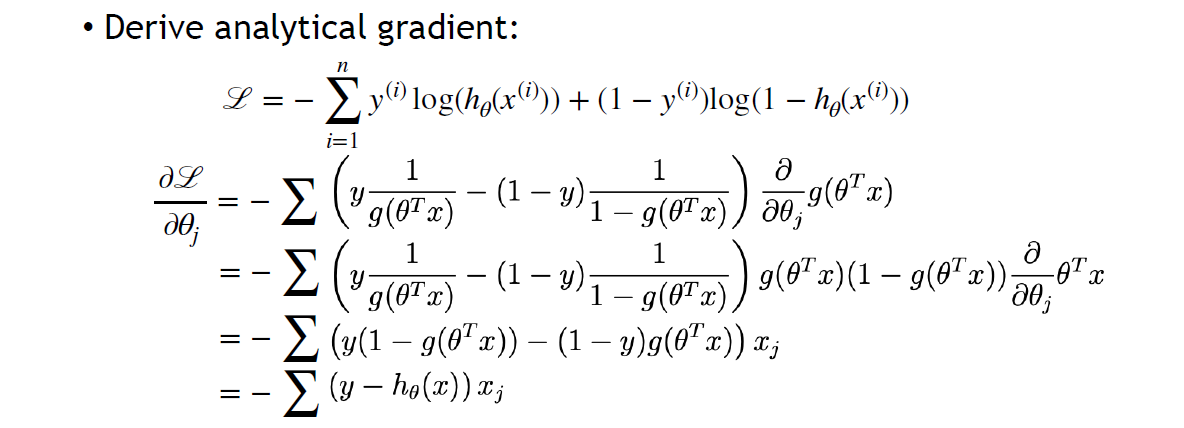
      3. 超参 weight initialization，会很大地影响收敛到的 local minima
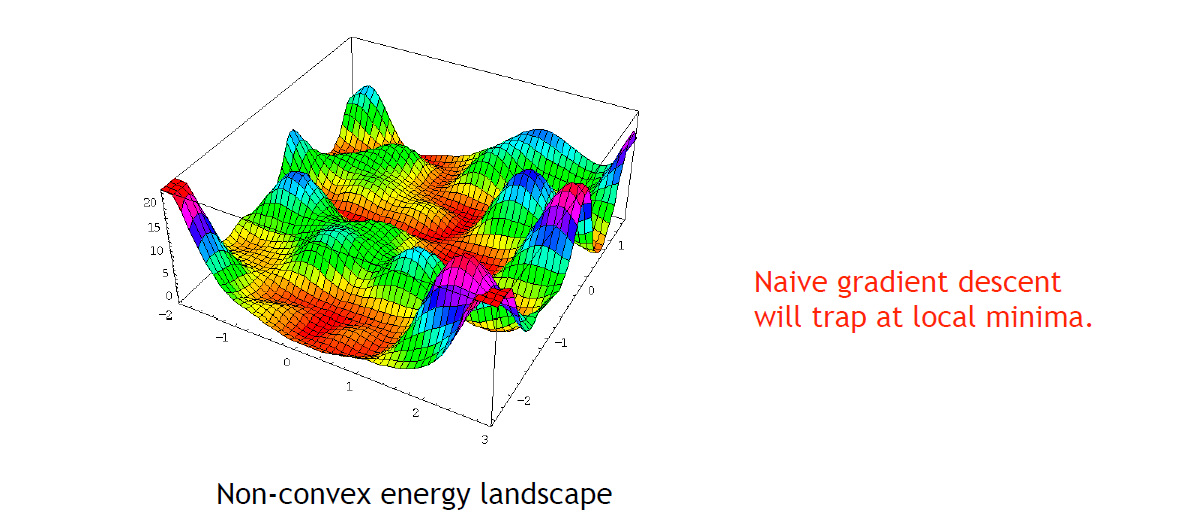
   5. 补救方法(最简单的)
      1. Batch Gradient Descent：对一个 batch(16/64/128) 求 gradient，这将使得gradient在全局gradient基础上增加一个噪声，使得descent可以跳出较浅的local minima；
      2. Stochastic Gradient Descent：选择mini-batch，从所有数据中随机选择 N pairs as a batch and compute the average gradient from them
         1. +: fast
         2. +: can get out of local minima
6. Testing
   1. 分割Dataset |------------Training Dataset------------|--Testing Dataset--|
   2. 「高考应该考新题，不考见过的题」
   3. 用 NLL 评判 Testing Dataset 吗？模型最后 Evaluate 的应该是 classification accuracy，NLL 不直观甚至可能与 accuracy 冲突
   4. 泛化能力 Generalization gap

为什么不用 accuracy 做 loss？Non-Differentiability 的准确率是离散的不可微的无法反向传播的，轻微调整参数无法跳出local minima的，对置信度不敏感的

结语

简单分类方法 Logistic Regression 的局限性：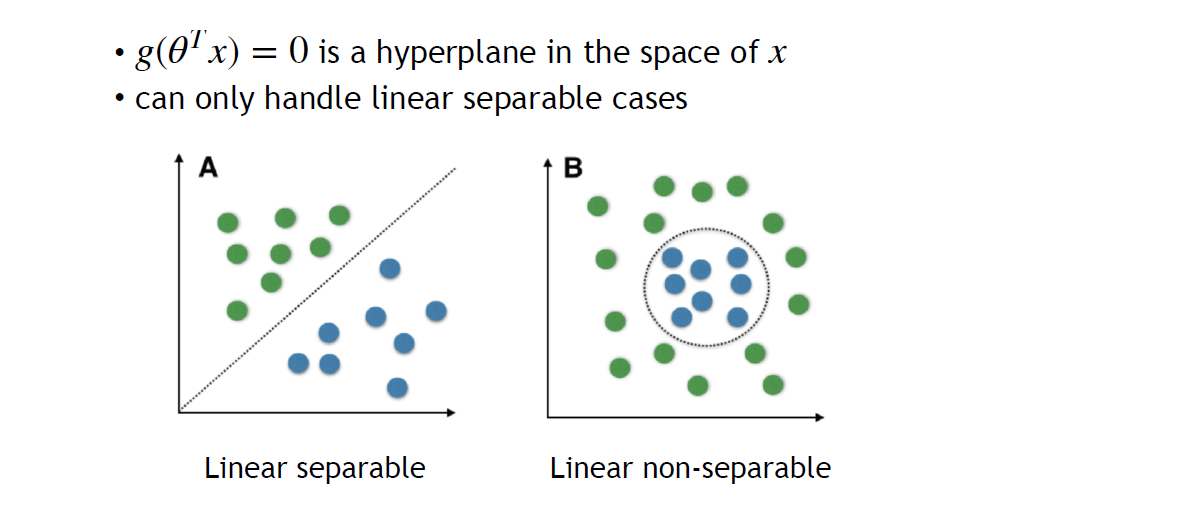
选择的点积函数 \displaystyle \theta^Tx 是一个 hyperplane，只能处理线性可分问题.

本次我们学习了

• Machine Learning 的范式：Prepare data -> Build model -> Optimization -> Test
• 在 Build model 中只涉及了单层线性函数，结果只能处理线性问题，令人失望：下次将要开始拓展神经网络 Model