本节是另一课程的内容,但也可以视为 CV 导论从 Classic Vision II 那一节的一个补充
SIFT
早在遇到语义分割以前,传统 CV 在处理目标识别的 equivariance 的问题时就已经举步维艰,但仍然有一些很不错的方法;我们首先回顾希望目标识别满足的 equivariance:
- scale
- rotation
- lighting
SIFT/Scale Invariant Feature Transform/尺度不变特征转换是较好地实现上面这几个等变性的一种方法。
关键点检测
LoG
对连续二元函数 f(x, y),其 Laplacian 算子是 \begin{aligned} \nabla \cdot {\nabla{f}} = \frac{\partial^2{f}}{\partial{x^2}}+ \frac{\partial^2{f}}{\partial{y^2}}\end{aligned},对离散二元函数 img,可以用卷积核 I = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0\end{bmatrix} 代替它;Laplacian 算子可以用来定位局部极值点,从而寻找 edge 或 key point
但是,Laplacian 算子同样能定位噪点,这会很大干扰结果,所以自然地想到先求 Gaussian 核平滑的结果;合并两步,我们只需求 Gaussian 核函数的 Laplacian 算子得到 LoG 算子:
DoG
Gaussian 函数 \displaystyle G(x,y,\sigma) = \frac{1}{2\pi }\sigma^{-2} e^{-\frac{x^2 + y^2}{2} \sigma^{-2}} 对 \sigma 求导得到
注意到 \displaystyle \frac{\partial{G}}{\partial{\sigma}} = \sigma \text{LoG},进一步推导有
这表明对两个不同方差的 Gaussian 函数求差(Diff of Gaussian, DoG)就能近似求 LoG,它的计算负担小于求 LoG
到今天大家不怎么在乎这点计算负担了
SIFT
简单了解这一工程实现,实现细节偶有差异,我们并不特别在乎。
高斯金字塔
从另一个角度说,启发自人眼近大远小、模糊远方的特征,我们想建立一种图像的尺度空间,满足在这个尺度空间上越远,就越模糊,越保留轮廓而抹去细节;高斯金字塔是这样一种尺度空间,采取了以下策略
- 近大远小:下采样(其实就是池化 Pooling)
- 模糊远方:高斯核 \displaystyle G(x, y, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{x^2 + y^2}{2 \sigma^2}} 平滑:L(x, y, \sigma) = G(x, y, \sigma) \otimes I(x, y)
具体地,采取了以下方式
- 金字塔层数 O = [\log_2 \min(h, w)] - 2
- 每一个 octave 有 6 层尺寸相同,模糊系数 \sigma 不同的图像
- 每一个 octave 之间下采样 2 倍
Key points localization
- 阈值化:去除较小的噪点和一些不稳定点
- DoG 寻找极值点:在每个 Octave 中,和 (x, y, \sigma) 三个方向上周围的 26 个点比较,找到极值点
- 三元二阶泰勒展开找到亚像素精度的极值点位置
- 阈值化:去掉对比度不够的点
- 去除边缘效应
- 确定极值点方向:在 1.5 倍尺度为半径的圆内的所有像素(邻域窗口),高斯滤波加权,梯度方向多数投票
生成关键点描述符
我们现在有每个关键点的方向,需要给出一个特征向量描述这个关键点
- 邻域窗口旋转至关键点方向
- 邻域窗口划分为 4x4 子块
- 每个窗口内计算 8 个方向的梯度直方图
- 得到 128 维特征向量
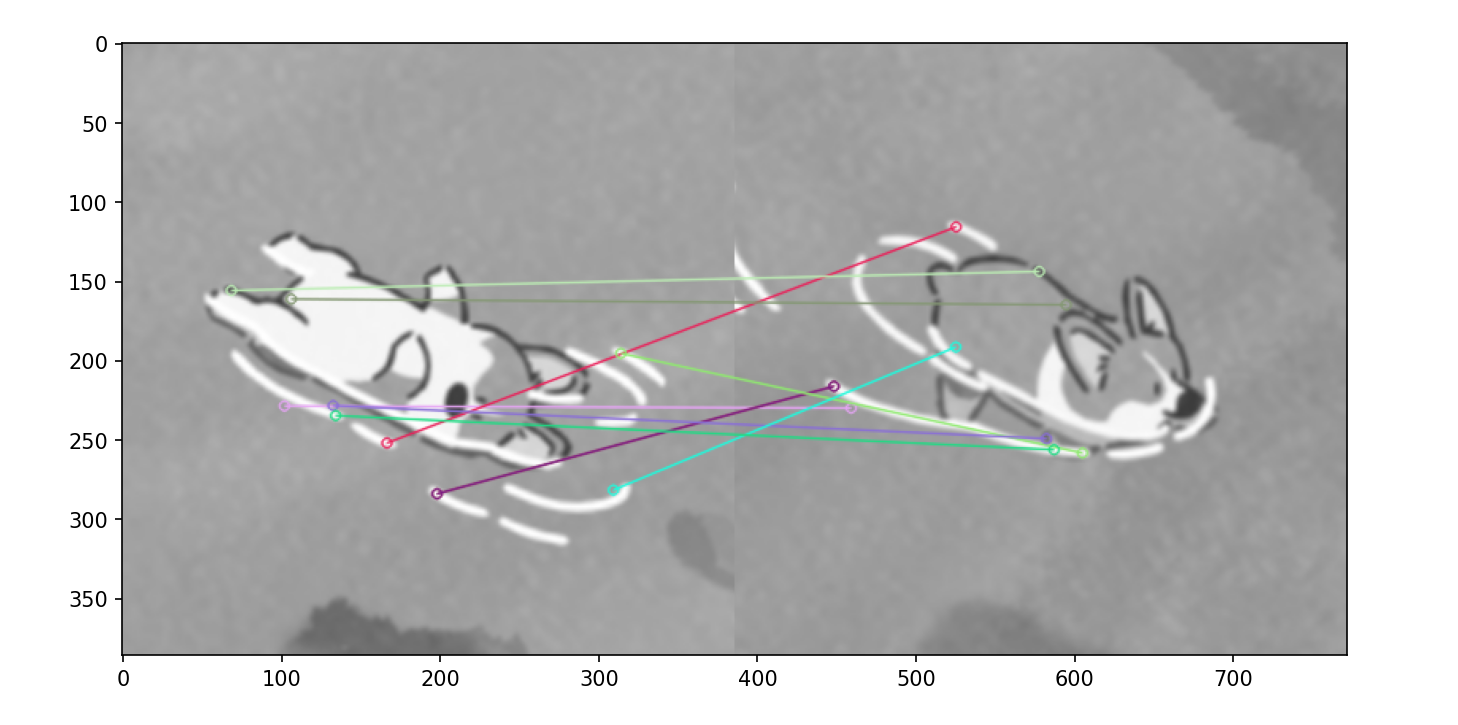
匹配
最后,可以通过 SIFT 描述符的距离衡量两幅图像的相似程度
实现
很高兴 OpenCV 能直接实现它!
import cv2
from matplotlib import pyplot as plt
img = ...
sift = cv2.SIFT_create()
keypoints, descriptors = sift.detectAndCompute(img, None)
img_with_kps = cv2.drawKeypoints(img, keypoints, None, flag=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
plt.figure()
plt.imshow(img_with_kps, cmap='gray')
plt.show()

匹配
直接使用 BFMatcher
kp1, desc1 = sift.detectAndCompute(img1, None)
kp2, desc2 = sift.detectAndCompute(img2, None)
bf = cv2.BFMatcher(cv2.NORM_L2, crossCheck=True)
matches = bf.match(desc1, desc2)
matches = sorted(matches, key=lambda x: x.distance)
matched_img = cv2.drawMatches(
img1, kp1,
img2, kp2,
matches[:10],
None,
flags=cv2.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS
)
plt.figure()
plt.imshow(matched_img, cmap='gray')
plt.show()
HOG
HOG/Histograms of Oriented Gradients/方向梯度直方图思想类似,过程相对简单:
- 图像灰度化
- 采用 Gamma 校正法进行对比度均衡
- 将图像划分为(例如 6x6)的小 cells
- 统计每个 cell 的梯度直方图,形成每个 cell 的 descriptor
- 将(例如 3x3 个)cell 组成一个 block,在 block 上再进行一次对比度均衡并将所有 cell 的 descriptor 组成该 block 的 HOG 特征
- 将 img 的所有 block 的 HOG 特征组成该 img 的 HOG 特征向量 (blocks, cells, bins)
2 是为了对光照和阴影有 invariance
将 HOG 与 SVM 组合可以得到一个目标分类器
实现
opencv 提供了 HOG 方法和预训练的用于行人检测的 SVM 分类器:
import cv2
from matplotlib import pyplot as plt
img = cv2.imread('pedestrian.jpg')
img = cv2.resize(img, fx=0.5, fy=0.5, dsize=None)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
hog = cv2.HOGDescriptor()
hog.setSVMDetector(cv2.HOGDescriptor_getDefaultPeopleDetector())
boxes, weights = hog.detectMultiScale(gray, winStride=(8, 8), padding=(8, 8), scale=1.05)
for (x, y, w, h) in boxes:
cv2.rectangle(img, (x, y), (x + w, y + h), (0, 255, 0), 2)
plt.figure()
plt.imshow(img)
plt.show()

或者使用 scikit-image 库
from skimage import feature as ft
img = cv2.imread('pedestrian.jpg', cv2.IMREAD_GRAYSCALE)
features = ft.hog(img,orientations=6, pixels_per_cell=[6, 6], cells_per_block=[3, 3], visualize=True)
plt.imshow(features[1], cmap='gray')
plt.show()
